Continuously-Tempered PDMP Samplers

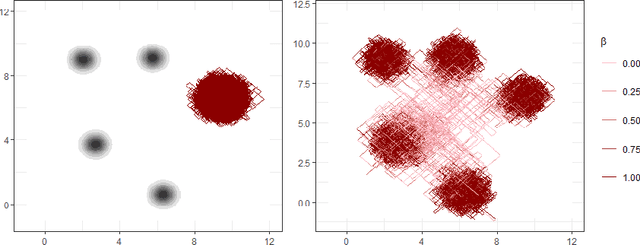
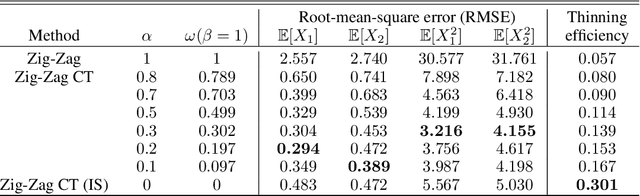
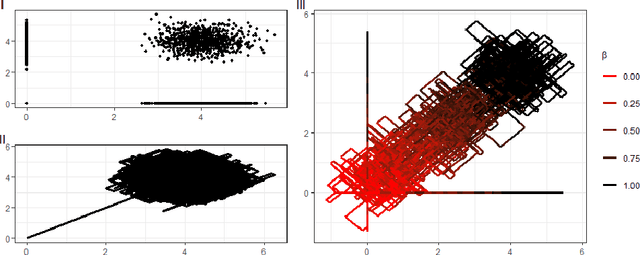
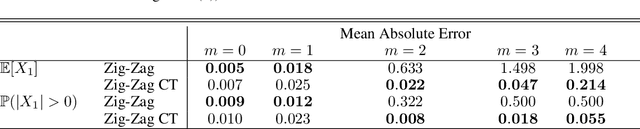
New sampling algorithms based on simulating continuous-time stochastic processes called piece-wise deterministic Markov processes (PDMPs) have shown considerable promise. However, these methods can struggle to sample from multi-modal or heavy-tailed distributions. We show how tempering ideas can improve the mixing of PDMPs in such cases. We introduce an extended distribution defined over the state of the posterior distribution and an inverse temperature, which interpolates between a tractable distribution when the inverse temperature is 0 and the posterior when the inverse temperature is 1. The marginal distribution of the inverse temperature is a mixture of a continuous distribution on [0,1) and a point mass at 1: which means that we obtain samples when the inverse temperature is 1, and these are draws from the posterior, but sampling algorithms will also explore distributions at lower temperatures which will improve mixing. We show how PDMPs, and particularly the Zig-Zag sampler, can be implemented to sample from such an extended distribution. The resulting algorithm is easy to implement and we show empirically that it can outperform existing PDMP-based samplers on challenging multimodal posteriors.

Efficient computation of the volume of a polytope in high-dimensions using Piecewise Deterministic Markov Processes

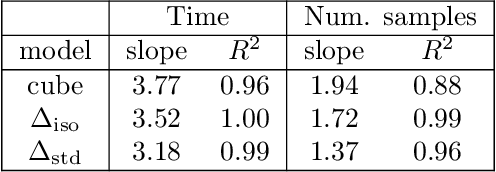
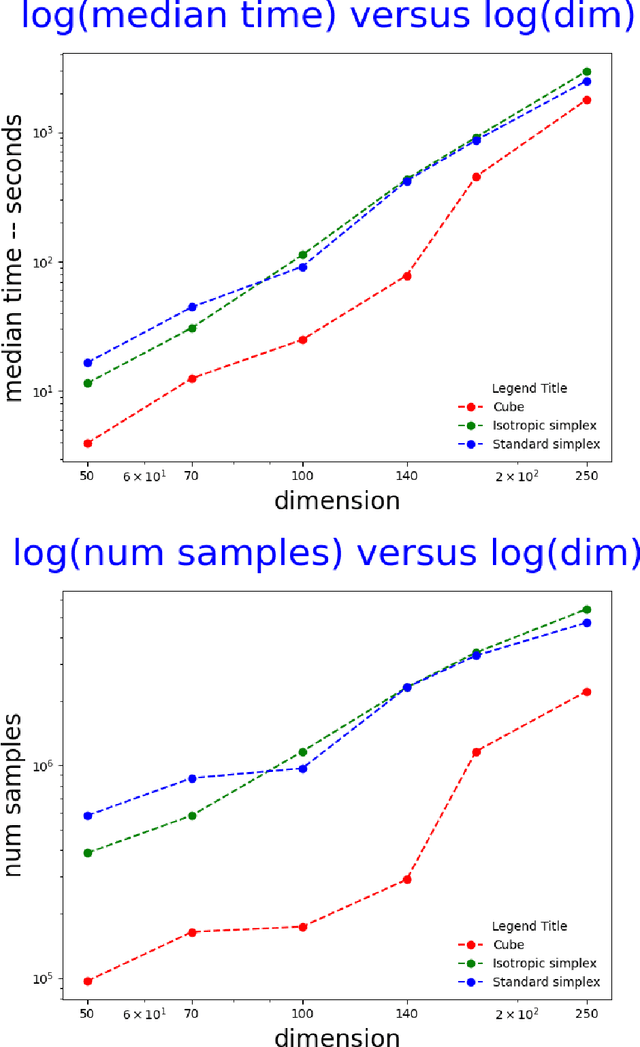
Computing the volume of a polytope in high dimensions is computationally challenging but has wide applications. Current state-of-the-art algorithms to compute such volumes rely on efficient sampling of a Gaussian distribution restricted to the polytope, using e.g. Hamiltonian Monte Carlo. We present a new sampling strategy that uses a Piecewise Deterministic Markov Process. Like Hamiltonian Monte Carlo, this new method involves simulating trajectories of a non-reversible process and inherits similar good mixing properties. However, importantly, the process can be simulated more easily due to its piecewise linear trajectories - and this leads to a reduction of the computational cost by a factor of the dimension of the space. Our experiments indicate that our method is numerically robust and is one order of magnitude faster (or better) than existing methods using Hamiltonian Monte Carlo. On a single core processor, we report computational time of a few minutes up to dimension 500.

Reversible Jump PDMP Samplers for Variable Selection

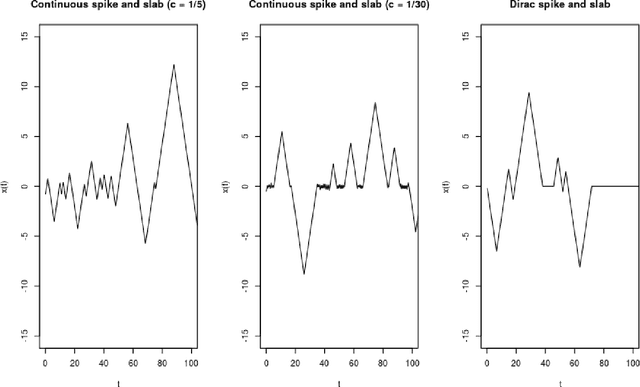
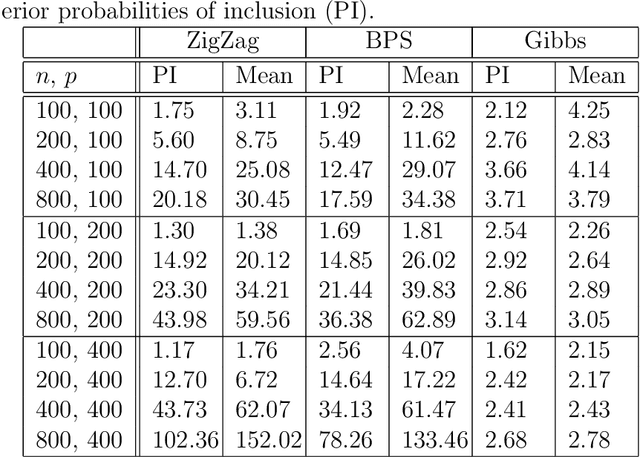
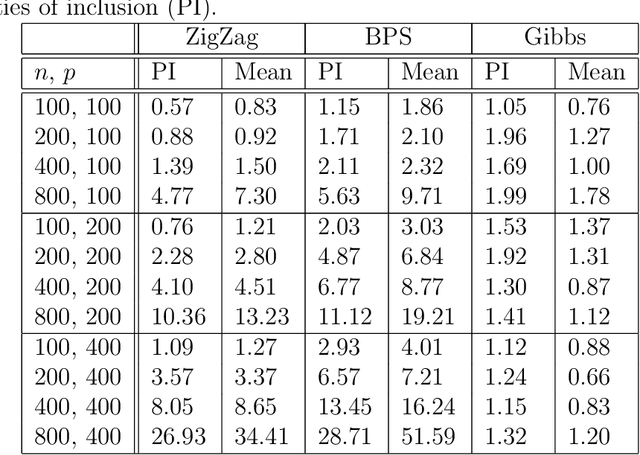
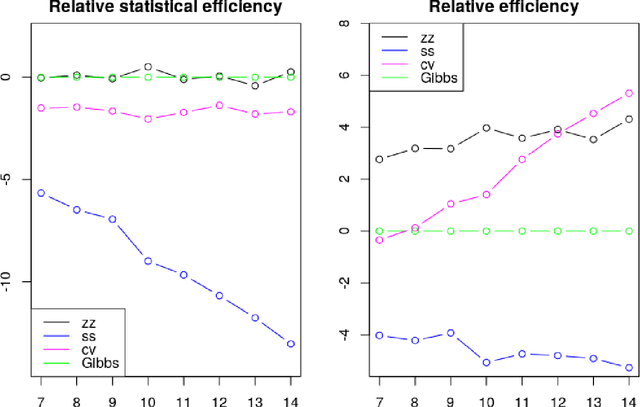
A new class of Markov chain Monte Carlo (MCMC) algorithms, based on simulating piecewise deterministic Markov processes (PDMPs), have recently shown great promise: they are non-reversible, can mix better than standard MCMC algorithms, and can use subsampling ideas to speed up computation in big data scenarios. However, current PDMP samplers can only sample from posterior densities that are differentiable almost everywhere, which precludes their use for model choice. Motivated by variable selection problems, we show how to develop reversible jump PDMP samplers that can jointly explore the discrete space of models and the continuous space of parameters. Our framework is general: it takes any existing PDMP sampler, and adds two types of trans-dimensional moves that allow for the addition or removal of a variable from the model. We show how the rates of these trans-dimensional moves can be calculated so that the sampler has the correct invariant distribution. Simulations show that the new samplers can mix better than standard MCMC algorithms. Our empirical results show they are also more efficient than gradient-based samplers that avoid model choice through use of continuous spike-and-slab priors which replace a point mass at zero for each parameter with a density concentrated around zero.