Efficient computation of the volume of a polytope in high-dimensions using Piecewise Deterministic Markov Processes

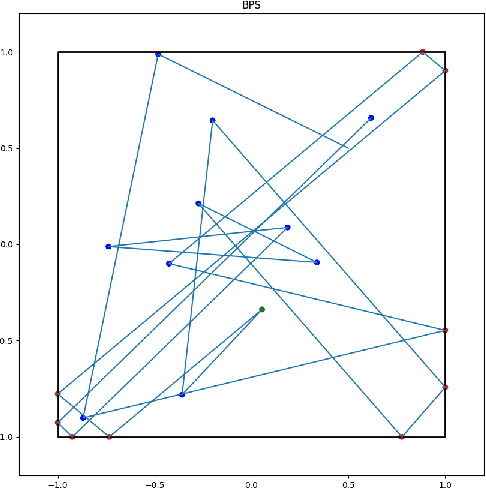
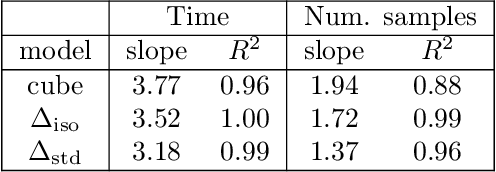
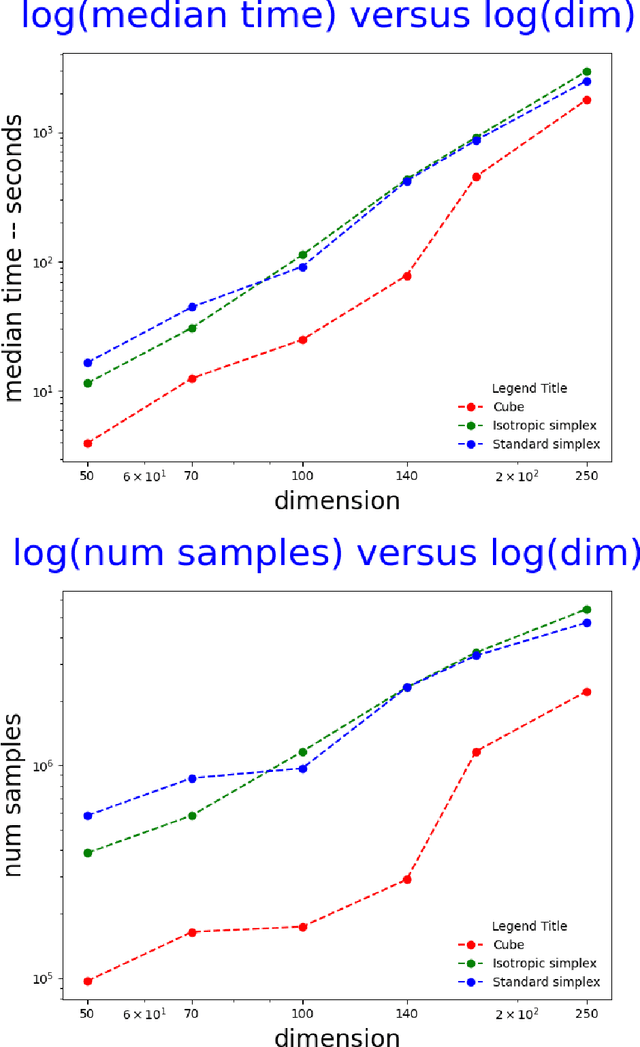
Computing the volume of a polytope in high dimensions is computationally challenging but has wide applications. Current state-of-the-art algorithms to compute such volumes rely on efficient sampling of a Gaussian distribution restricted to the polytope, using e.g. Hamiltonian Monte Carlo. We present a new sampling strategy that uses a Piecewise Deterministic Markov Process. Like Hamiltonian Monte Carlo, this new method involves simulating trajectories of a non-reversible process and inherits similar good mixing properties. However, importantly, the process can be simulated more easily due to its piecewise linear trajectories - and this leads to a reduction of the computational cost by a factor of the dimension of the space. Our experiments indicate that our method is numerically robust and is one order of magnitude faster (or better) than existing methods using Hamiltonian Monte Carlo. On a single core processor, we report computational time of a few minutes up to dimension 500.

kd-switch: A Universal Online Predictor with an application to Sequential Two-Sample Testing

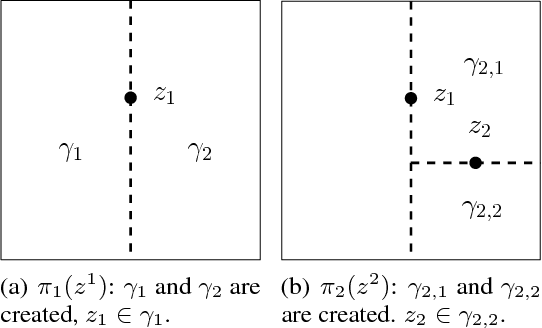
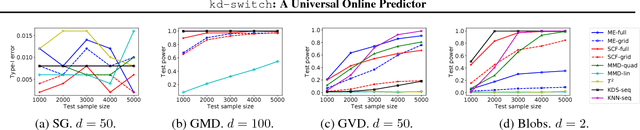
We propose a novel online predictor for discrete labels conditioned on multivariate features in $\mathbb{R}^d$. The predictor is pointwise universal: it achieves a normalized log loss performance asymptotically as good as the true conditional entropy of the labels given the features. The predictor is based on a feature space discretization induced by a full-fledged k-d tree with randomly picked directions and a switch distribution, requiring no hyperparameter setting and automatically selecting the most relevant scales in the feature space. Using recent results, a consistent sequential two-sample test is built from this predictor. In terms of discrimination power, on selected challenging datasets, it is comparable to or better than state-of-the-art non-sequential two-sample tests based on the train-test paradigm and, a recent sequential test requiring hyperparameters. The time complexity to process the $n$-th sample point is $O(\log n)$ in probability (with respect to the distribution generating the data points), in contrast to the linear complexity of the previous sequential approach.