A Cramér Distance perspective on Non-crossing Quantile Regression in Distributional Reinforcement Learning

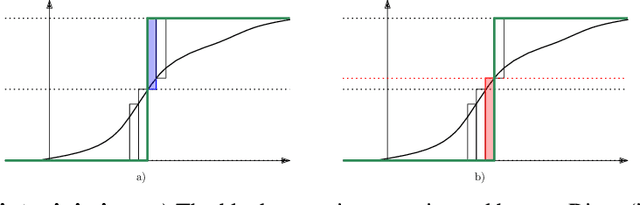
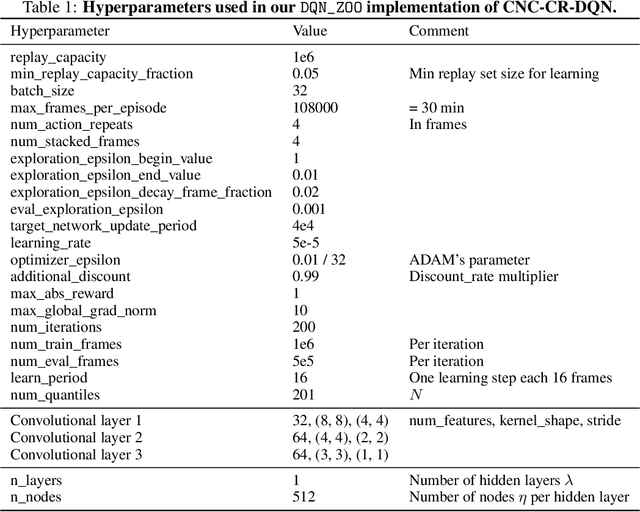
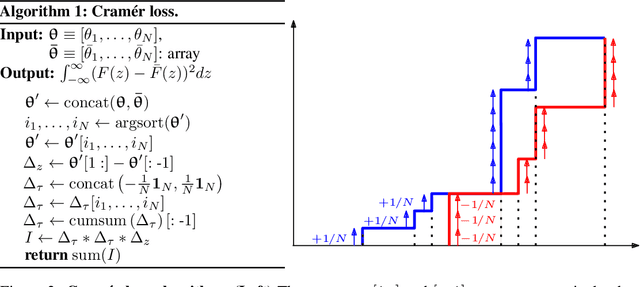
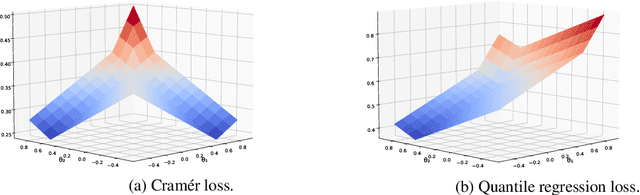
Distributional reinforcement learning (DRL) extends the value-based approach by using a deep convolutional network to approximate the full distribution over future returns instead of the mean only, providing a richer signal that leads to improved performances. Quantile-based methods like QR-DQN project arbitrary distributions onto a parametric subset of staircase distributions by minimizing the 1-Wasserstein distance, however, due to biases in the gradients, the quantile regression loss is used instead for training, guaranteeing the same minimizer and enjoying unbiased gradients. Recently, monotonicity constraints on the quantiles have been shown to improve the performance of QR-DQN for uncertainty-based exploration strategies. The contribution of this work is in the setting of fixed quantile levels and is twofold. First, we prove that the Cram\'er distance yields a projection that coincides with the 1-Wasserstein one and that, under monotonicity constraints, the squared Cram\'er and the quantile regression losses yield collinear gradients, shedding light on the connection between these important elements of DRL. Second, we propose a novel non-crossing neural architecture that allows a good training performance using a novel algorithm to compute the Cram\'er distance, yielding significant improvements over QR-DQN in a number of games of the standard Atari 2600 benchmark.

PCMC-Net: Feature-based Pairwise Choice Markov Chains

Pairwise Choice Markov Chains (PCMC) have been recently introduced to overcome limitations of choice models based on traditional axioms unable to express empirical observations from modern behavior economics like framing effects and asymmetric dominance. The inference approach that estimates the transition rates between each possible pair of alternatives via maximum likelihood suffers when the examples of each alternative are scarce and is inappropriate when new alternatives can be observed at test time. In this work, we propose an amortized inference approach for PCMC by embedding its definition into a neural network that represents transition rates as a function of the alternatives' and individual's features. We apply our construction to the complex case of airline itinerary booking where singletons are common (due to varying prices and individual-specific itineraries), and asymmetric dominance and behaviors strongly dependent on market segments are observed. Experiments show our network significantly outperforming, in terms of prediction accuracy and logarithmic loss, feature engineered standard and latent class Multinomial Logit models as well as recent machine learning approaches.

kd-switch: A Universal Online Predictor with an application to Sequential Two-Sample Testing

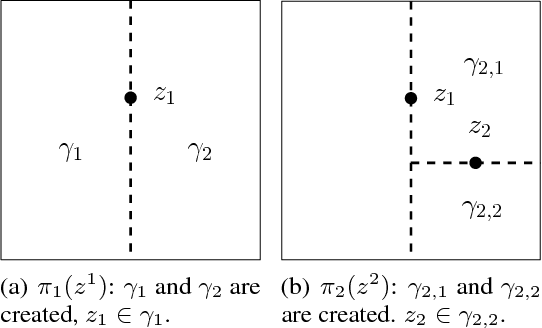
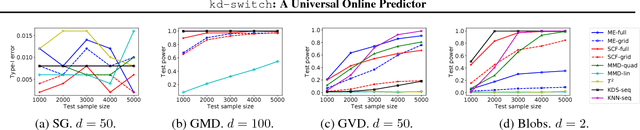
We propose a novel online predictor for discrete labels conditioned on multivariate features in $\mathbb{R}^d$. The predictor is pointwise universal: it achieves a normalized log loss performance asymptotically as good as the true conditional entropy of the labels given the features. The predictor is based on a feature space discretization induced by a full-fledged k-d tree with randomly picked directions and a switch distribution, requiring no hyperparameter setting and automatically selecting the most relevant scales in the feature space. Using recent results, a consistent sequential two-sample test is built from this predictor. In terms of discrimination power, on selected challenging datasets, it is comparable to or better than state-of-the-art non-sequential two-sample tests based on the train-test paradigm and, a recent sequential test requiring hyperparameters. The time complexity to process the $n$-th sample point is $O(\log n)$ in probability (with respect to the distribution generating the data points), in contrast to the linear complexity of the previous sequential approach.