kd-switch: A Universal Online Predictor with an application to Sequential Two-Sample Testing
Paper and Code
Jan 23, 2019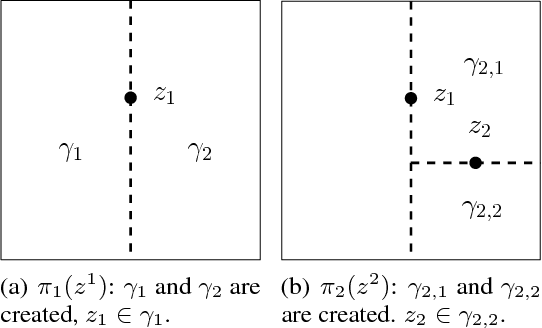
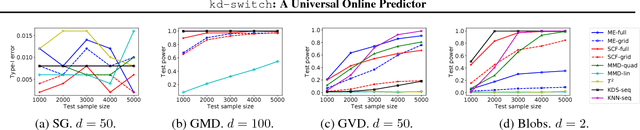
We propose a novel online predictor for discrete labels conditioned on multivariate features in $\mathbb{R}^d$. The predictor is pointwise universal: it achieves a normalized log loss performance asymptotically as good as the true conditional entropy of the labels given the features. The predictor is based on a feature space discretization induced by a full-fledged k-d tree with randomly picked directions and a switch distribution, requiring no hyperparameter setting and automatically selecting the most relevant scales in the feature space. Using recent results, a consistent sequential two-sample test is built from this predictor. In terms of discrimination power, on selected challenging datasets, it is comparable to or better than state-of-the-art non-sequential two-sample tests based on the train-test paradigm and, a recent sequential test requiring hyperparameters. The time complexity to process the $n$-th sample point is $O(\log n)$ in probability (with respect to the distribution generating the data points), in contrast to the linear complexity of the previous sequential approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge