Tengyao Wang
Deep learning with missing data
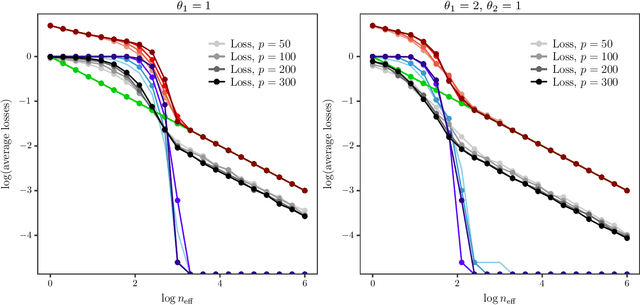
Apr 21, 2025Abstract:In the context of multivariate nonparametric regression with missing covariates, we propose Pattern Embedded Neural Networks (PENNs), which can be applied in conjunction with any existing imputation technique. In addition to a neural network trained on the imputed data, PENNs pass the vectors of observation indicators through a second neural network to provide a compact representation. The outputs are then combined in a third neural network to produce final predictions. Our main theoretical result exploits an assumption that the observation patterns can be partitioned into cells on which the Bayes regression function behaves similarly, and belongs to a compositional H\"older class. It provides a finite-sample excess risk bound that holds for an arbitrary missingness mechanism, and in combination with a complementary minimax lower bound, demonstrates that our PENN estimator attains in typical cases the minimax rate of convergence as if the cells of the partition were known in advance, up to a poly-logarithmic factor in the sample size. Numerical experiments on simulated, semi-synthetic and real data confirm that the PENN estimator consistently improves, often dramatically, on standard neural networks without pattern embedding. Code to reproduce our experiments, as well as a tutorial on how to apply our method, is publicly available.
Sharp-SSL: Selective high-dimensional axis-aligned random projections for semi-supervised learning
Apr 18, 2023Abstract:We propose a new method for high-dimensional semi-supervised learning problems based on the careful aggregation of the results of a low-dimensional procedure applied to many axis-aligned random projections of the data. Our primary goal is to identify important variables for distinguishing between the classes; existing low-dimensional methods can then be applied for final class assignment. Motivated by a generalized Rayleigh quotient, we score projections according to the traces of the estimated whitened between-class covariance matrices on the projected data. This enables us to assign an importance weight to each variable for a given projection, and to select our signal variables by aggregating these weights over high-scoring projections. Our theory shows that the resulting Sharp-SSL algorithm is able to recover the signal coordinates with high probability when we aggregate over sufficiently many random projections and when the base procedure estimates the whitened between-class covariance matrix sufficiently well. The Gaussian EM algorithm is a natural choice as a base procedure, and we provide a new analysis of its performance in semi-supervised settings that controls the parameter estimation error in terms of the proportion of labeled data in the sample. Numerical results on both simulated data and a real colon tumor dataset support the excellent empirical performance of the method.
Automatic Change-Point Detection in Time Series via Deep Learning
Nov 07, 2022Abstract:Detecting change-points in data is challenging because of the range of possible types of change and types of behaviour of data when there is no change. Statistically efficient methods for detecting a change will depend on both of these features, and it can be difficult for a practitioner to develop an appropriate detection method for their application of interest. We show how to automatically generate new detection methods based on training a neural network. Our approach is motivated by many existing tests for the presence of a change-point being able to be represented by a simple neural network, and thus a neural network trained with sufficient data should have performance at least as good as these methods. We present theory that quantifies the error rate for such an approach, and how it depends on the amount of training data. Empirical results show that, even with limited training data, its performance is competitive with the standard CUSUM test for detecting a change in mean when the noise is independent and Gaussian, and can substantially outperform it in the presence of auto-correlated or heavy-tailed noise. Our method also shows strong results in detecting and localising changes in activity based on accelerometer data.
AIM 2020 Challenge on Rendering Realistic Bokeh
Nov 10, 2020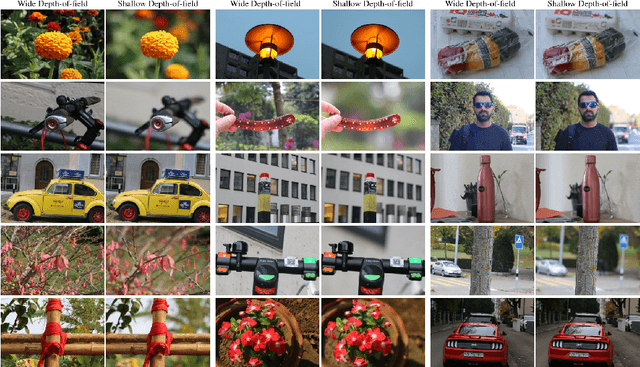


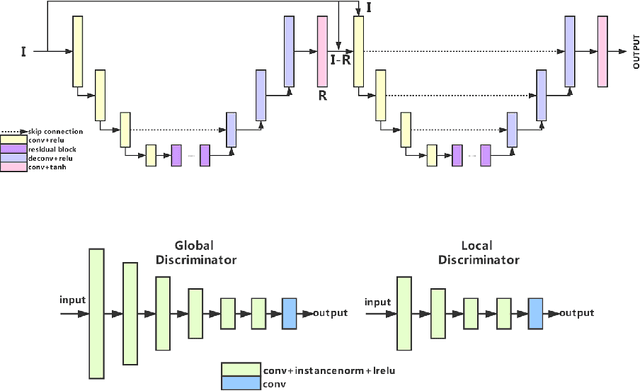
Abstract:This paper reviews the second AIM realistic bokeh effect rendering challenge and provides the description of the proposed solutions and results. The participating teams were solving a real-world bokeh simulation problem, where the goal was to learn a realistic shallow focus technique using a large-scale EBB! bokeh dataset consisting of 5K shallow / wide depth-of-field image pairs captured using the Canon 7D DSLR camera. The participants had to render bokeh effect based on only one single frame without any additional data from other cameras or sensors. The target metric used in this challenge combined the runtime and the perceptual quality of the solutions measured in the user study. To ensure the efficiency of the submitted models, we measured their runtime on standard desktop CPUs as well as were running the models on smartphone GPUs. The proposed solutions significantly improved the baseline results, defining the state-of-the-art for practical bokeh effect rendering problem.
High-dimensional, multiscale online changepoint detection
Mar 07, 2020



Abstract:We introduce a new method for high-dimensional, online changepoint detection in settings where a $p$-variate Gaussian data stream may undergo a change in mean. The procedure works by performing likelihood ratio tests against simple alternatives of different scales in each coordinate, and then aggregating test statistics across scales and coordinates. The algorithm is online in the sense that its worst-case computational complexity per new observation, namely $O\bigl(p^2 \log (ep)\bigr)$, is independent of the number of previous observations; in practice, it may even be significantly faster than this. We prove that the patience, or average run length under the null, of our procedure is at least at the desired nominal level, and provide guarantees on its response delay under the alternative that depend on the sparsity of the vector of mean change. Simulations confirm the practical effectiveness of our proposal.
Sparse principal component analysis via random projections
Jul 24, 2018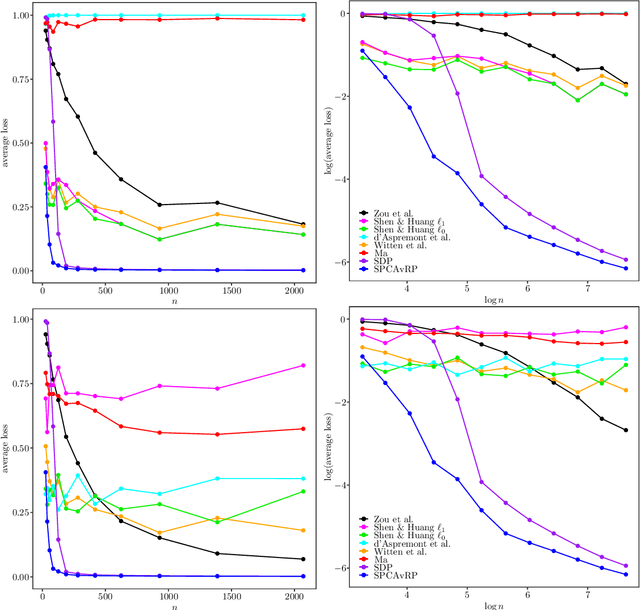
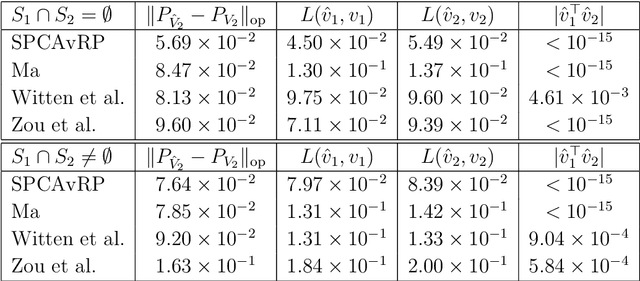
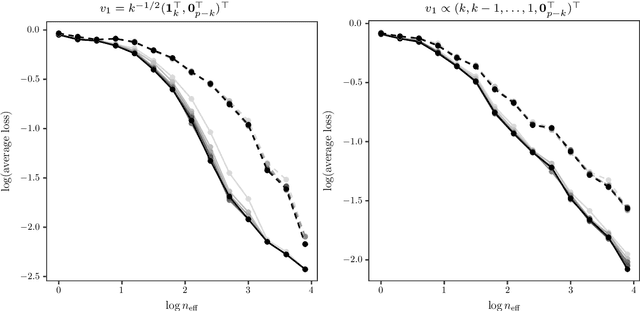
Abstract:We introduce a new method for sparse principal component analysis, based on the aggregation of eigenvector information from carefully-selected random projections of the sample covariance matrix. Unlike most alternative approaches, our algorithm is non-iterative, so is not vulnerable to a bad choice of initialisation. Our theory provides great detail on the statistical and computational trade-off in our procedure, revealing a subtle interplay between the effective sample size and the number of random projections that are required to achieve the minimax optimal rate. Numerical studies provide further insight into the procedure and confirm its highly competitive finite-sample performance.
Statistical and computational trade-offs in estimation of sparse principal components
Sep 28, 2016

Abstract:In recent years, sparse principal component analysis has emerged as an extremely popular dimension reduction technique for high-dimensional data. The theoretical challenge, in the simplest case, is to estimate the leading eigenvector of a population covariance matrix under the assumption that this eigenvector is sparse. An impressive range of estimators have been proposed; some of these are fast to compute, while others are known to achieve the minimax optimal rate over certain Gaussian or sub-Gaussian classes. In this paper, we show that, under a widely-believed assumption from computational complexity theory, there is a fundamental trade-off between statistical and computational performance in this problem. More precisely, working with new, larger classes satisfying a restricted covariance concentration condition, we show that there is an effective sample size regime in which no randomised polynomial time algorithm can achieve the minimax optimal rate. We also study the theoretical performance of a (polynomial time) variant of the well-known semidefinite relaxation estimator, revealing a subtle interplay between statistical and computational efficiency.
* Published at http://dx.doi.org/10.1214/15-AOS1369 in the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
Average-case Hardness of RIP Certification
May 31, 2016
Abstract:The restricted isometry property (RIP) for design matrices gives guarantees for optimal recovery in sparse linear models. It is of high interest in compressed sensing and statistical learning. This property is particularly important for computationally efficient recovery methods. As a consequence, even though it is in general NP-hard to check that RIP holds, there have been substantial efforts to find tractable proxies for it. These would allow the construction of RIP matrices and the polynomial-time verification of RIP given an arbitrary matrix. We consider the framework of average-case certifiers, that never wrongly declare that a matrix is RIP, while being often correct for random instances. While there are such functions which are tractable in a suboptimal parameter regime, we show that this is a computationally hard task in any better regime. Our results are based on a new, weaker assumption on the problem of detecting dense subgraphs.
Multiple Identifications in Multi-Armed Bandits
May 14, 2012

Abstract:We study the problem of identifying the top $m$ arms in a multi-armed bandit game. Our proposed solution relies on a new algorithm based on successive rejects of the seemingly bad arms, and successive accepts of the good ones. This algorithmic contribution allows to tackle other multiple identifications settings that were previously out of reach. In particular we show that this idea of successive accepts and rejects applies to the multi-bandit best arm identification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge