Nitin Viswanathan
Using Poisson Binomial GLMs to Reveal Voter Preferences
Feb 04, 2018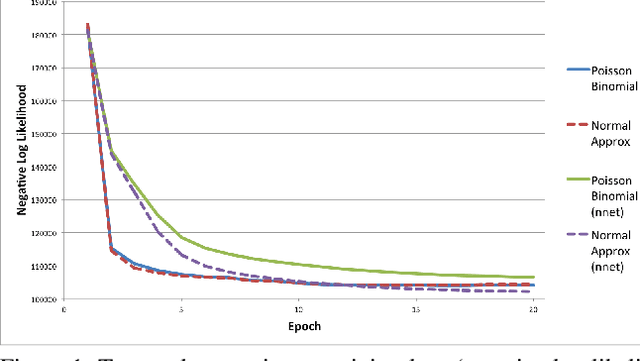
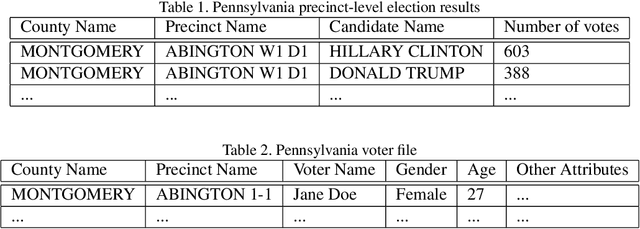
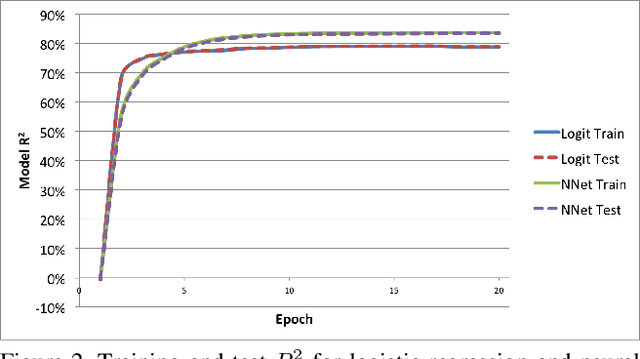
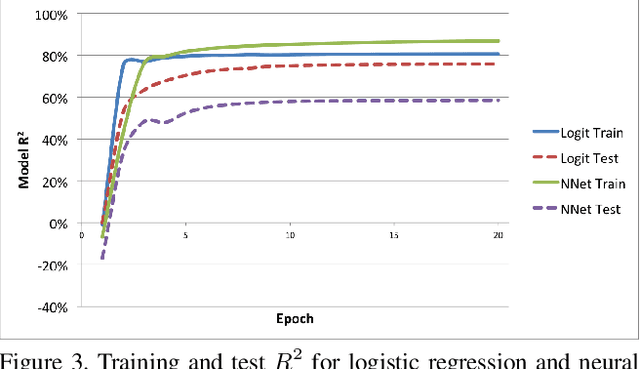
Abstract:We present a new modeling technique for solving the problem of ecological inference, in which individual-level associations are inferred from labeled data available only at the aggregate level. We model aggregate count data as arising from the Poisson binomial, the distribution of the sum of independent but not identically distributed Bernoulli random variables. We relate individual-level probabilities to individual covariates using both a logistic regression and a neural network. A normal approximation is derived via the Lyapunov Central Limit Theorem, allowing us to efficiently fit these models on large datasets. We apply this technique to the problem of revealing voter preferences in the 2016 presidential election, fitting a model to a sample of over four million voters from the highly contested swing state of Pennsylvania. We validate the model at the precinct level via a holdout set, and at the individual level using weak labels, finding that the model is predictive and it learns intuitively reasonable associations.
Multiple Identifications in Multi-Armed Bandits
May 14, 2012

Abstract:We study the problem of identifying the top $m$ arms in a multi-armed bandit game. Our proposed solution relies on a new algorithm based on successive rejects of the seemingly bad arms, and successive accepts of the good ones. This algorithmic contribution allows to tackle other multiple identifications settings that were previously out of reach. In particular we show that this idea of successive accepts and rejects applies to the multi-bandit best arm identification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge