Optimized Partial Identification Bounds for Regression Discontinuity Designs with Manipulation

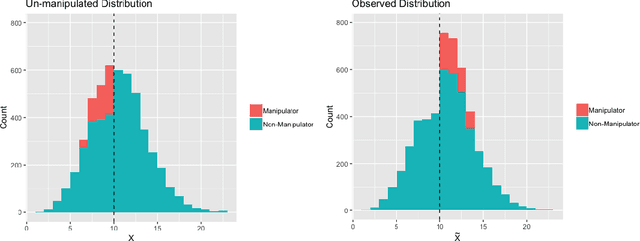
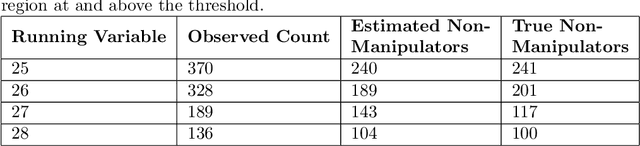
The regression discontinuity (RD) design is one of the most popular quasi-experimental methods for applied causal inference. In practice, the method is quite sensitive to the assumption that individuals cannot control their value of a "running variable" that determines treatment status precisely. If individuals are able to precisely manipulate their scores, then point identification is lost. We propose a procedure for obtaining partial identification bounds in the case of a discrete running variable where manipulation is present. Our method relies on two stages: first, we derive the distribution of non-manipulators under several assumptions about the data. Second, we obtain bounds on the causal effect via a sequential convex programming approach. We also propose methods for tightening the partial identification bounds using an auxiliary covariate, and derive confidence intervals via the bootstrap. We demonstrate the utility of our method on a simulated dataset.

Some New Results for Poisson Binomial Models

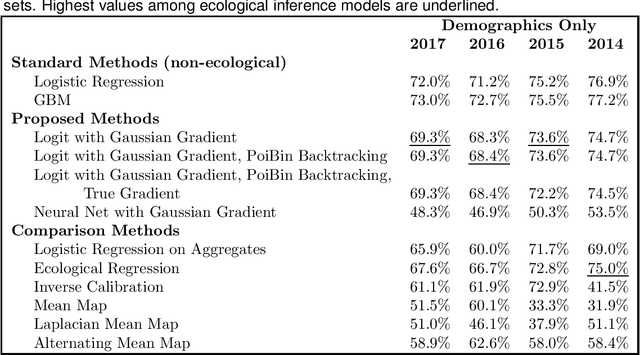
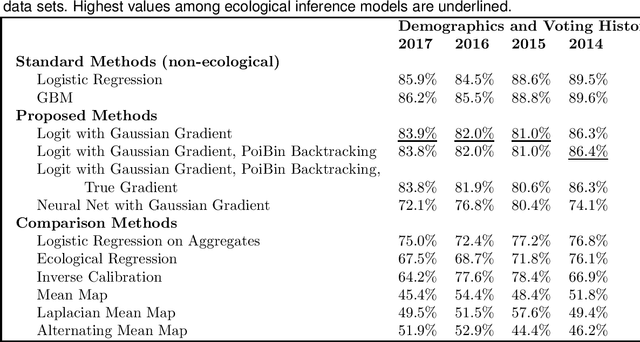
We consider a problem of ecological inference, in which individual-level covariates are known, but labeled data is available only at the aggregate level. The intended application is modeling voter preferences in elections. In Rosenman and Viswanathan (2018), we proposed modeling individual voter probabilities via a logistic regression, and posing the problem as a maximum likelihood estimation for the parameter vector beta. The likelihood is a Poisson binomial, the distribution of the sum of independent but not identically distributed Bernoulli variables, though we approximate it with a heteroscedastic Gaussian for computational efficiency. Here, we extend the prior work by proving results about the existence of the MLE and the curvature of this likelihood, which is not log-concave in general. We further demonstrate the utility of our method on a real data example. Using data on voters in Morris County, NJ, we demonstrate that our approach outperforms other ecological inference methods in predicting a related, but known outcome: whether an individual votes.

Using Poisson Binomial GLMs to Reveal Voter Preferences

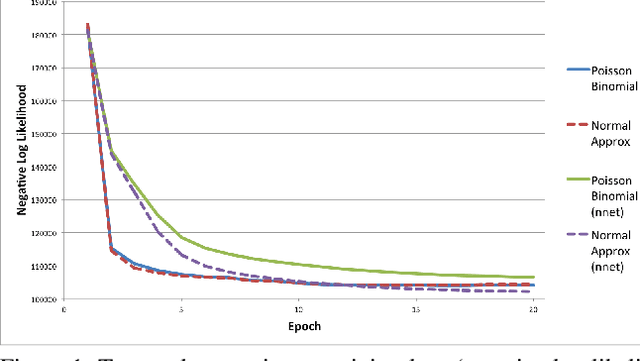
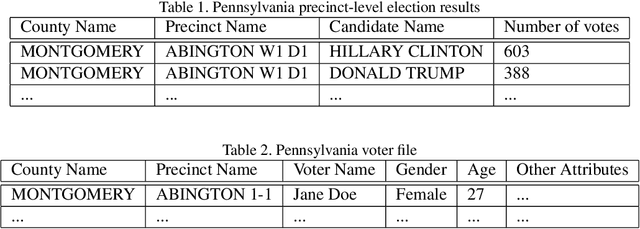
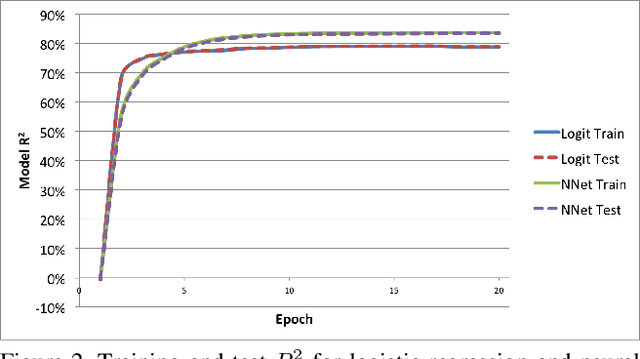
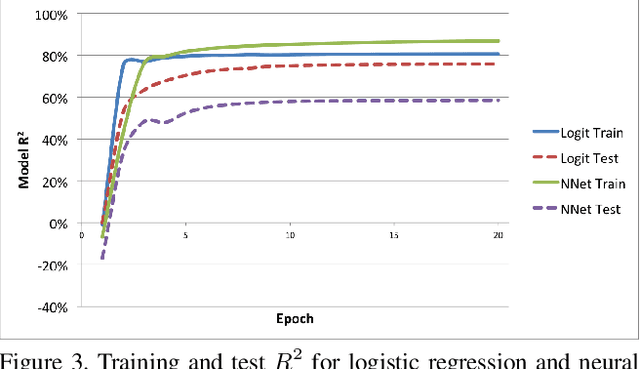
We present a new modeling technique for solving the problem of ecological inference, in which individual-level associations are inferred from labeled data available only at the aggregate level. We model aggregate count data as arising from the Poisson binomial, the distribution of the sum of independent but not identically distributed Bernoulli random variables. We relate individual-level probabilities to individual covariates using both a logistic regression and a neural network. A normal approximation is derived via the Lyapunov Central Limit Theorem, allowing us to efficiently fit these models on large datasets. We apply this technique to the problem of revealing voter preferences in the 2016 presidential election, fitting a model to a sample of over four million voters from the highly contested swing state of Pennsylvania. We validate the model at the precinct level via a holdout set, and at the individual level using weak labels, finding that the model is predictive and it learns intuitively reasonable associations.