Some New Results for Poisson Binomial Models
Paper and Code
Jul 21, 2019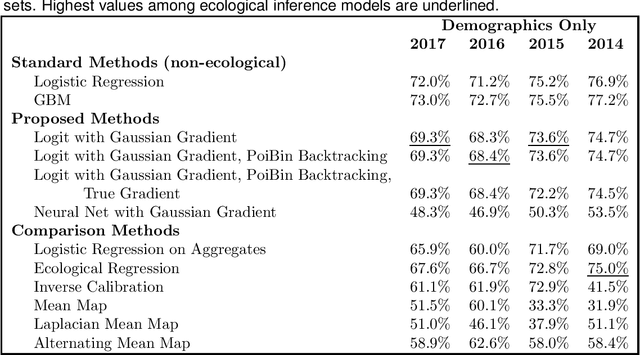
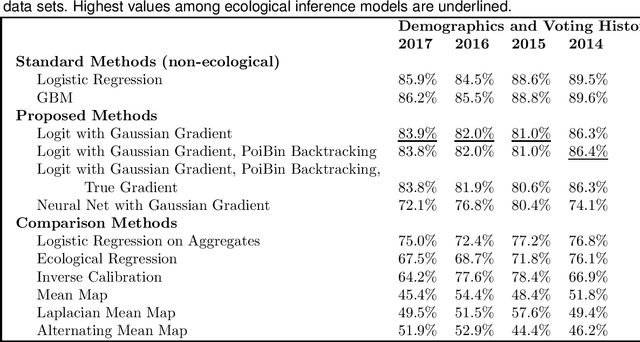
We consider a problem of ecological inference, in which individual-level covariates are known, but labeled data is available only at the aggregate level. The intended application is modeling voter preferences in elections. In Rosenman and Viswanathan (2018), we proposed modeling individual voter probabilities via a logistic regression, and posing the problem as a maximum likelihood estimation for the parameter vector beta. The likelihood is a Poisson binomial, the distribution of the sum of independent but not identically distributed Bernoulli variables, though we approximate it with a heteroscedastic Gaussian for computational efficiency. Here, we extend the prior work by proving results about the existence of the MLE and the curvature of this likelihood, which is not log-concave in general. We further demonstrate the utility of our method on a real data example. Using data on voters in Morris County, NJ, we demonstrate that our approach outperforms other ecological inference methods in predicting a related, but known outcome: whether an individual votes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge