Karthik Rajkumar
Optimized Partial Identification Bounds for Regression Discontinuity Designs with Manipulation
Oct 04, 2019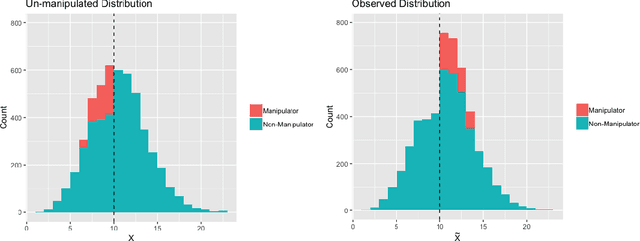
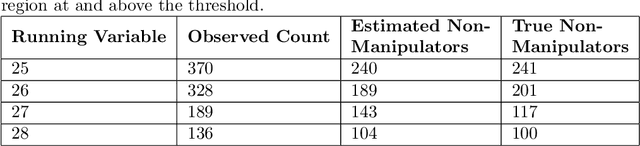


Abstract:The regression discontinuity (RD) design is one of the most popular quasi-experimental methods for applied causal inference. In practice, the method is quite sensitive to the assumption that individuals cannot control their value of a "running variable" that determines treatment status precisely. If individuals are able to precisely manipulate their scores, then point identification is lost. We propose a procedure for obtaining partial identification bounds in the case of a discrete running variable where manipulation is present. Our method relies on two stages: first, we derive the distribution of non-manipulators under several assumptions about the data. Second, we obtain bounds on the causal effect via a sequential convex programming approach. We also propose methods for tightening the partial identification bounds using an auxiliary covariate, and derive confidence intervals via the bootstrap. We demonstrate the utility of our method on a simulated dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge