Sharp-SSL: Selective high-dimensional axis-aligned random projections for semi-supervised learning

We propose a new method for high-dimensional semi-supervised learning problems based on the careful aggregation of the results of a low-dimensional procedure applied to many axis-aligned random projections of the data. Our primary goal is to identify important variables for distinguishing between the classes; existing low-dimensional methods can then be applied for final class assignment. Motivated by a generalized Rayleigh quotient, we score projections according to the traces of the estimated whitened between-class covariance matrices on the projected data. This enables us to assign an importance weight to each variable for a given projection, and to select our signal variables by aggregating these weights over high-scoring projections. Our theory shows that the resulting Sharp-SSL algorithm is able to recover the signal coordinates with high probability when we aggregate over sufficiently many random projections and when the base procedure estimates the whitened between-class covariance matrix sufficiently well. The Gaussian EM algorithm is a natural choice as a base procedure, and we provide a new analysis of its performance in semi-supervised settings that controls the parameter estimation error in terms of the proportion of labeled data in the sample. Numerical results on both simulated data and a real colon tumor dataset support the excellent empirical performance of the method.

Generalized sampling with functional principal components for high-resolution random field estimation

In this paper, we take a statistical approach to the problem of recovering a function from low-resolution measurements taken with respect to an arbitrary basis, by regarding the function of interest as a realization of a random field. We introduce an infinite-dimensional framework for high-resolution estimation of a random field from its low-resolution indirect measurements as well as the high-resolution measurements of training observations by merging the existing frameworks of generalized sampling and functional principal component analysis. We study the statistical performance of the resulting estimation procedure and show that high-resolution recovery is indeed possible provided appropriate low-rank and angle conditions hold and provided the training set is sufficiently large relative to the desired resolution. We also consider sparse representations of the principle components, which can reduce the required size of the training set. Furthermore, the effectiveness of the proposed procedure is investigated in various numerical examples.

Sparse principal component analysis via random projections

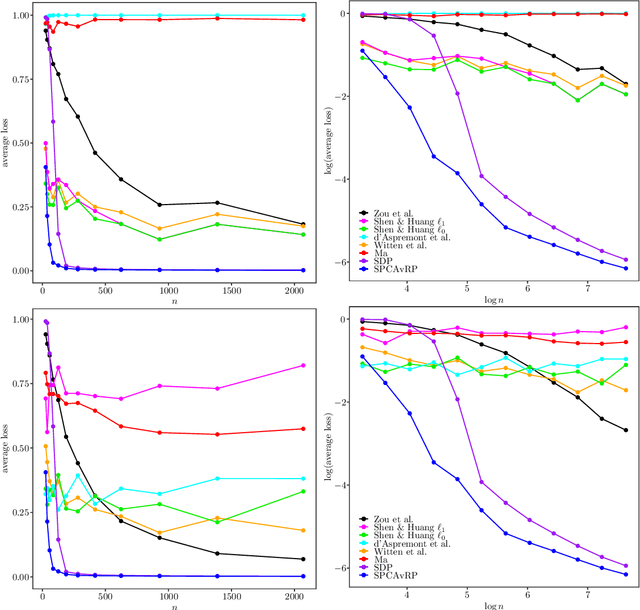
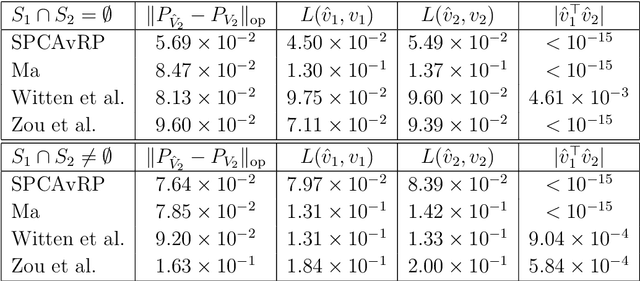
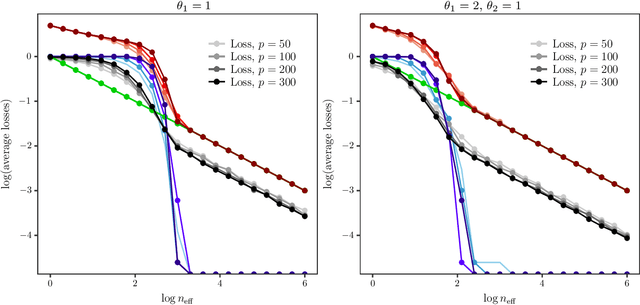
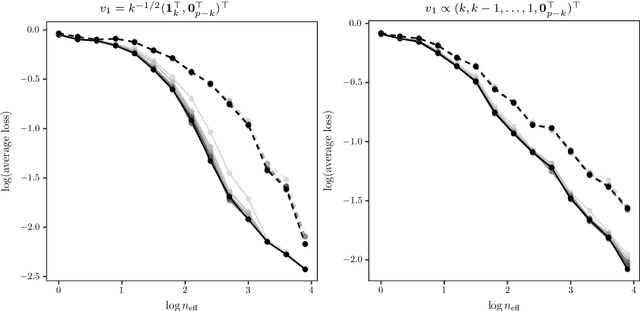
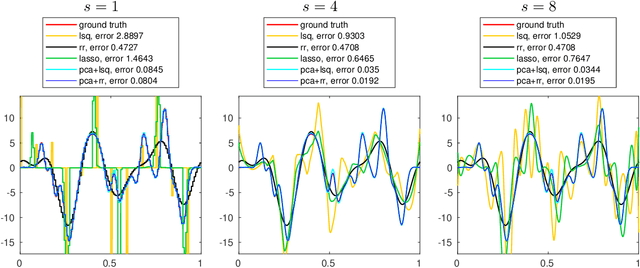
We introduce a new method for sparse principal component analysis, based on the aggregation of eigenvector information from carefully-selected random projections of the sample covariance matrix. Unlike most alternative approaches, our algorithm is non-iterative, so is not vulnerable to a bad choice of initialisation. Our theory provides great detail on the statistical and computational trade-off in our procedure, revealing a subtle interplay between the effective sample size and the number of random projections that are required to achieve the minimax optimal rate. Numerical studies provide further insight into the procedure and confirm its highly competitive finite-sample performance.