Generalized sampling with functional principal components for high-resolution random field estimation

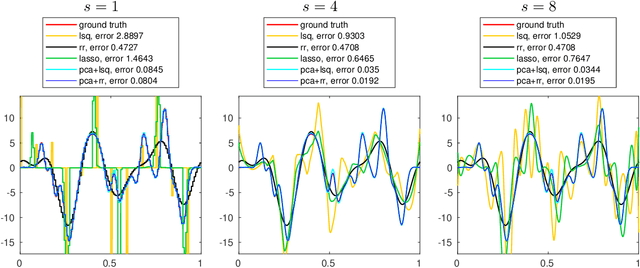
In this paper, we take a statistical approach to the problem of recovering a function from low-resolution measurements taken with respect to an arbitrary basis, by regarding the function of interest as a realization of a random field. We introduce an infinite-dimensional framework for high-resolution estimation of a random field from its low-resolution indirect measurements as well as the high-resolution measurements of training observations by merging the existing frameworks of generalized sampling and functional principal component analysis. We study the statistical performance of the resulting estimation procedure and show that high-resolution recovery is indeed possible provided appropriate low-rank and angle conditions hold and provided the training set is sufficiently large relative to the desired resolution. We also consider sparse representations of the principle components, which can reduce the required size of the training set. Furthermore, the effectiveness of the proposed procedure is investigated in various numerical examples.