Geometric-Based Pruning Rules For Change Point Detection in Multiple Independent Time Series

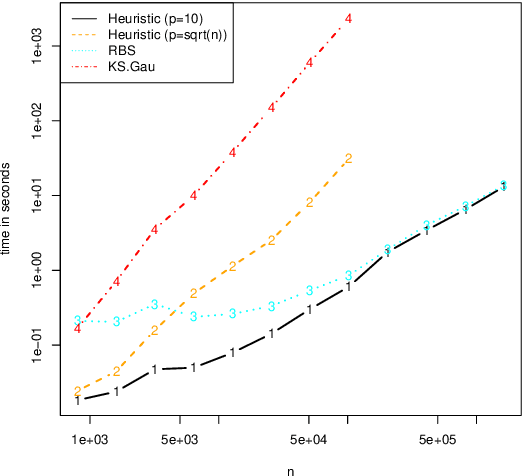
We consider the problem of detecting multiple changes in multiple independent time series. The search for the best segmentation can be expressed as a minimization problem over a given cost function. We focus on dynamic programming algorithms that solve this problem exactly. When the number of changes is proportional to data length, an inequality-based pruning rule encoded in the PELT algorithm leads to a linear time complexity. Another type of pruning, called functional pruning, gives a close-to-linear time complexity whatever the number of changes, but only for the analysis of univariate time series. We propose a few extensions of functional pruning for multiple independent time series based on the use of simple geometric shapes (balls and hyperrectangles). We focus on the Gaussian case, but some of our rules can be easily extended to the exponential family. In a simulation study we compare the computational efficiency of different geometric-based pruning rules. We show that for small dimensions (2, 3, 4) some of them ran significantly faster than inequality-based approaches in particular when the underlying number of changes is small compared to the data length.

Fast Online Changepoint Detection via Functional Pruning CUSUM statistics

Many modern applications of online changepoint detection require the ability to process high-frequency observations, sometimes with limited available computational resources. Online algorithms for detecting a change in mean often involve using a moving window, or specifying the expected size of change. Such choices affect which changes the algorithms have most power to detect. We introduce an algorithm, Functional Online CuSUM (FOCuS), which is equivalent to running these earlier methods simultaneously for all sizes of window, or all possible values for the size of change. Our theoretical results give tight bounds on the expected computational cost per iteration of FOCuS, with this being logarithmic in the number of observations. We show how FOCuS can be applied to a number of different change in mean scenarios, and demonstrate its practical utility through its state-of-the art performance at detecting anomalous behaviour in computer server data.

Increased peak detection accuracy in over-dispersed ChIP-seq data with supervised segmentation models

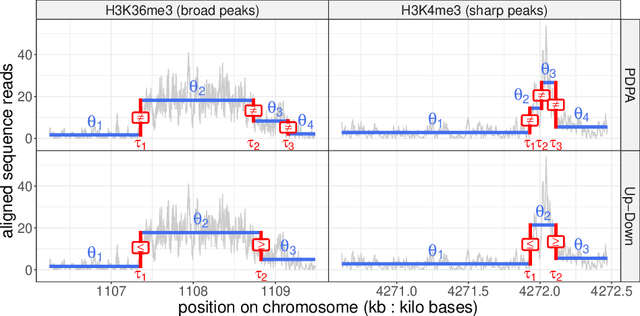
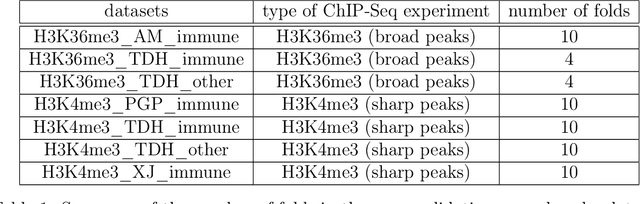
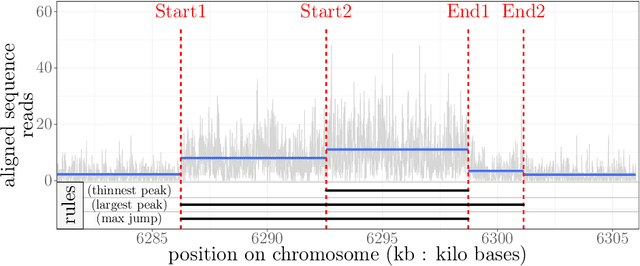
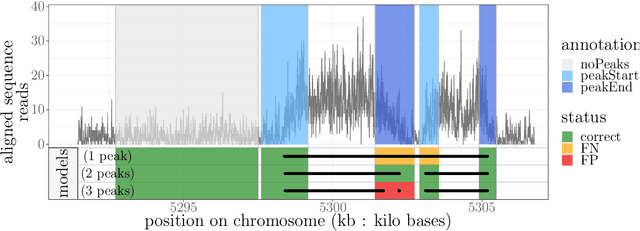
Motivation: Histone modification constitutes a basic mechanism for the genetic regulation of gene expression. In early 2000s, a powerful technique has emerged that couples chromatin immunoprecipitation with high-throughput sequencing (ChIP-seq). This technique provides a direct survey of the DNA regions associated to these modifications. In order to realize the full potential of this technique, increasingly sophisticated statistical algorithms have been developed or adapted to analyze the massive amount of data it generates. Many of these algorithms were built around natural assumptions such as the Poisson one to model the noise in the count data. In this work we start from these natural assumptions and show that it is possible to improve upon them. Results: The results of our comparisons on seven reference datasets of histone modifications (H3K36me3 and H3K4me3) suggest that natural assumptions are not always realistic under application conditions. We show that the unconstrained multiple changepoint detection model, with alternative noise assumptions and a suitable setup, reduces the over-dispersion exhibited by count data and turns out to detect peaks more accurately than algorithms which rely on these natural assumptions.

New efficient algorithms for multiple change-point detection with kernels

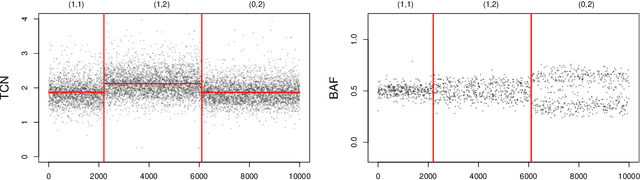
Several statistical approaches based on reproducing kernels have been proposed to detect abrupt changes arising in the full distribution of the observations and not only in the mean or variance. Some of these approaches enjoy good statistical properties (oracle inequality, \ldots). Nonetheless, they have a high computational cost both in terms of time and memory. This makes their application difficult even for small and medium sample sizes ($n< 10^4$). This computational issue is addressed by first describing a new efficient and exact algorithm for kernel multiple change-point detection with an improved worst-case complexity that is quadratic in time and linear in space. It allows dealing with medium size signals (up to $n \approx 10^5$). Second, a faster but approximation algorithm is described. It is based on a low-rank approximation to the Gram matrix. It is linear in time and space. This approximation algorithm can be applied to large-scale signals ($n \geq 10^6$). These exact and approximation algorithms have been implemented in \texttt{R} and \texttt{C} for various kernels. The computational and statistical performances of these new algorithms have been assessed through empirical experiments. The runtime of the new algorithms is observed to be faster than that of other considered procedures. Finally, simulations confirmed the higher statistical accuracy of kernel-based approaches to detect changes that are not only in the mean. These simulations also illustrate the flexibility of kernel-based approaches to analyze complex biological profiles made of DNA copy number and allele B frequencies. An R package implementing the approach will be made available on github.

Changepoint Detection in the Presence of Outliers

Many traditional methods for identifying changepoints can struggle in the presence of outliers, or when the noise is heavy-tailed. Often they will infer additional changepoints in order to fit the outliers. To overcome this problem, data often needs to be pre-processed to remove outliers, though this is difficult for applications where the data needs to be analysed online. We present an approach to changepoint detection that is robust to the presence of outliers. The idea is to adapt existing penalised cost approaches for detecting changes so that they use loss functions that are less sensitive to outliers. We argue that loss functions that are bounded, such as the classical biweight loss, are particularly suitable -- as we show that only bounded loss functions are robust to arbitrarily extreme outliers. We present an efficient dynamic programming algorithm that can find the optimal segmentation under our penalised cost criteria. Importantly, this algorithm can be used in settings where the data needs to be analysed online. We show that we can consistently estimate the number of changepoints, and accurately estimate their locations, using the biweight loss function. We demonstrate the usefulness of our approach for applications such as analysing well-log data, detecting copy number variation, and detecting tampering of wireless devices.

A log-linear time algorithm for constrained changepoint detection

Changepoint detection is a central problem in time series and genomic data. For some applications, it is natural to impose constraints on the directions of changes. One example is ChIP-seq data, for which adding an up-down constraint improves peak detection accuracy, but makes the optimization problem more complicated. We show how a recently proposed functional pruning technique can be adapted to solve such constrained changepoint detection problems. This leads to a new algorithm which can solve problems with arbitrary affine constraints on adjacent segment means, and which has empirical time complexity that is log-linear in the amount of data. This algorithm achieves state-of-the-art accuracy in a benchmark of several genomic data sets, and is orders of magnitude faster than existing algorithms that have similar accuracy. Our implementation is available as the PeakSegPDPA function in the coseg R package, https://github.com/tdhock/coseg