Approximate full conformal prediction in an RKHS

Full conformal prediction is a framework that implicitly formulates distribution-free confidence prediction regions for a wide range of estimators. However, a classical limitation of the full conformal framework is the computation of the confidence prediction regions, which is usually impossible since it requires training infinitely many estimators (for real-valued prediction for instance). The main purpose of the present work is to describe a generic strategy for designing a tight approximation to the full conformal prediction region that can be efficiently computed. Along with this approximate confidence region, a theoretical quantification of the tightness of this approximation is developed, depending on the smoothness assumptions on the loss and score functions. The new notion of thickness is introduced for quantifying the discrepancy between the approximate confidence region and the full conformal one.

Approximate full conformal prediction in RKHS

Full conformal prediction is a framework that implicitly formulates distribution-free confidence prediction regions for a wide range of estimators. However, a classical limitation of the full conformal framework is the computation of the confidence prediction regions, which is usually impossible since it requires training infinitely many estimators (for real-valued prediction for instance). The main purpose of the present work is to describe a generic strategy for designing a tight approximation to the full conformal prediction region that can be efficiently computed. Along with this approximate confidence region, a theoretical quantification of the tightness of this approximation is developed, depending on the smoothness assumptions on the loss and score functions. The new notion of thickness is introduced for quantifying the discrepancy between the approximate confidence region and the full conformal one.

Minimum discrepancy principle strategy for choosing $k$ in $k$-NN regression

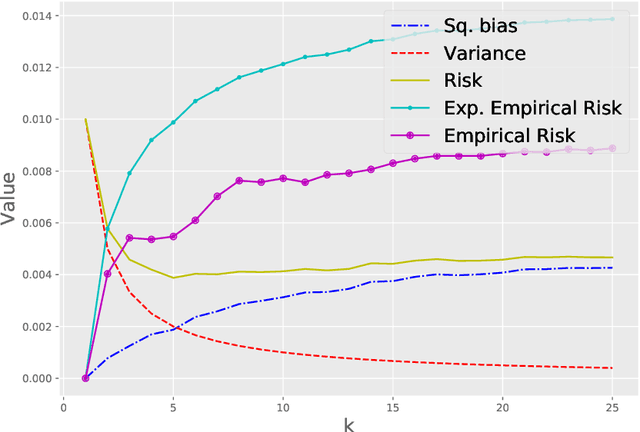
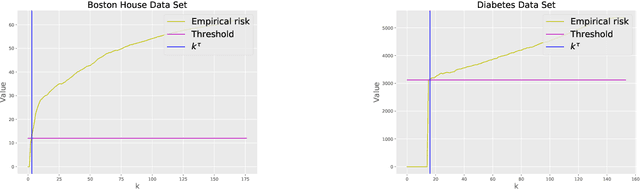
This paper presents a novel data-driven strategy to choose the hyperparameter $k$ in the $k$-NN regression estimator. We treat the problem of choosing the hyperparameter as an iterative procedure (over $k$) and propose using an easily implemented in practice strategy based on the idea of early stopping and the minimum discrepancy principle. This estimation strategy is proven to be minimax optimal, under the fixed-design assumption on covariates, over different smoothness function classes, for instance, the Lipschitz functions class on a bounded domain. After that, the novel strategy shows consistent simulations results on artificial and real-world data sets in comparison to other model selection strategies such as the Hold-out method.

Early stopping and polynomial smoothing in regression with reproducing kernels

In this paper we study the problem of early stopping for iterative learning algorithms in reproducing kernel Hilbert space (RKHS) in the nonparametric regression framework. In particular, we work with gradient descent and (iterative) kernel ridge regression algorithms. We present a data-driven rule to perform early stopping without a validation set that is based on the so-called minimum discrepancy principle. This method enjoys only one assumption on the regression function: it belongs to a reproducing kernel Hilbert space (RKHS). The proposed rule is proved to be minimax optimal over different types of kernel spaces, including finite rank and Sobolev smoothness classes. The proof is derived from the fixed-point analysis of the localized Rademacher complexities, which is a standard technique for obtaining optimal rates in the nonparametric regression literature. In addition to that, we present simulations results on artificial datasets that show comparable performance of the designed rule with respect to other stopping rules such as the one determined by V-fold cross-validation.

Analyzing the discrepancy principle for kernelized spectral filter learning algorithms

We investigate the construction of early stopping rules in the nonparametric regression problem where iterative learning algorithms are used and the optimal iteration number is unknown. More precisely, we study the discrepancy principle, as well as modifications based on smoothed residuals, for kernelized spectral filter learning algorithms including gradient descent. Our main theoretical bounds are oracle inequalities established for the empirical estimation error (fixed design), and for the prediction error (random design). From these finite-sample bounds it follows that the classical discrepancy principle is statistically adaptive for slow rates occurring in the hard learning scenario, while the smoothed discrepancy principles are adaptive over ranges of faster rates (resp. higher smoothness parameters). Our approach relies on deviation inequalities for the stopping rules in the fixed design setting, combined with change-of-norm arguments to deal with the random design setting.

New efficient algorithms for multiple change-point detection with kernels

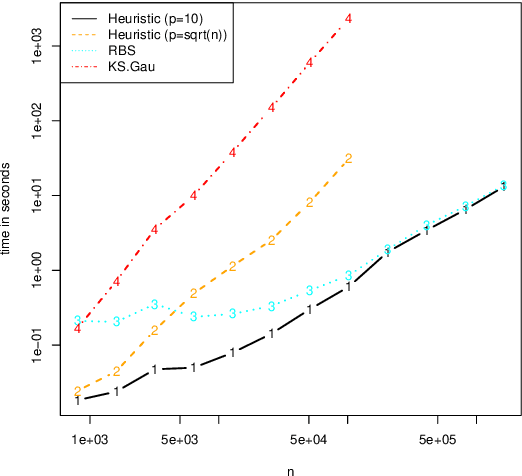
Several statistical approaches based on reproducing kernels have been proposed to detect abrupt changes arising in the full distribution of the observations and not only in the mean or variance. Some of these approaches enjoy good statistical properties (oracle inequality, \ldots). Nonetheless, they have a high computational cost both in terms of time and memory. This makes their application difficult even for small and medium sample sizes ($n< 10^4$). This computational issue is addressed by first describing a new efficient and exact algorithm for kernel multiple change-point detection with an improved worst-case complexity that is quadratic in time and linear in space. It allows dealing with medium size signals (up to $n \approx 10^5$). Second, a faster but approximation algorithm is described. It is based on a low-rank approximation to the Gram matrix. It is linear in time and space. This approximation algorithm can be applied to large-scale signals ($n \geq 10^6$). These exact and approximation algorithms have been implemented in \texttt{R} and \texttt{C} for various kernels. The computational and statistical performances of these new algorithms have been assessed through empirical experiments. The runtime of the new algorithms is observed to be faster than that of other considered procedures. Finally, simulations confirmed the higher statistical accuracy of kernel-based approaches to detect changes that are not only in the mean. These simulations also illustrate the flexibility of kernel-based approaches to analyze complex biological profiles made of DNA copy number and allele B frequencies. An R package implementing the approach will be made available on github.

Stability revisited: new generalisation bounds for the Leave-one-Out

The present paper provides a new generic strategy leading to non-asymptotic theoretical guarantees on the Leave-one-Out procedure applied to a broad class of learning algorithms. This strategy relies on two main ingredients: the new notion of $L^q$ stability, and the strong use of moment inequalities. $L^q$ stability extends the ongoing notion of hypothesis stability while remaining weaker than the uniform stability. It leads to new PAC exponential generalisation bounds for Leave-one-Out under mild assumptions. In the literature, such bounds are available only for uniform stable algorithms under boundedness for instance. Our generic strategy is applied to the Ridge regression algorithm as a first step.

A survey of cross-validation procedures for model selection

Used to estimate the risk of an estimator or to perform model selection, cross-validation is a widespread strategy because of its simplicity and its apparent universality. Many results exist on the model selection performances of cross-validation procedures. This survey intends to relate these results to the most recent advances of model selection theory, with a particular emphasis on distinguishing empirical statements from rigorous theoretical results. As a conclusion, guidelines are provided for choosing the best cross-validation procedure according to the particular features of the problem in hand.