Minimum discrepancy principle strategy for choosing $k$ in $k$-NN regression

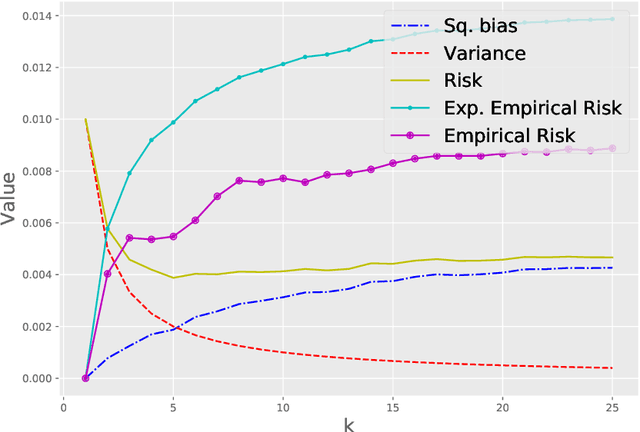
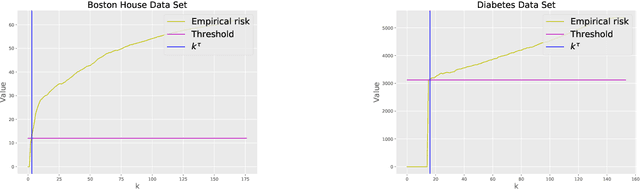
This paper presents a novel data-driven strategy to choose the hyperparameter $k$ in the $k$-NN regression estimator. We treat the problem of choosing the hyperparameter as an iterative procedure (over $k$) and propose using an easily implemented in practice strategy based on the idea of early stopping and the minimum discrepancy principle. This estimation strategy is proven to be minimax optimal, under the fixed-design assumption on covariates, over different smoothness function classes, for instance, the Lipschitz functions class on a bounded domain. After that, the novel strategy shows consistent simulations results on artificial and real-world data sets in comparison to other model selection strategies such as the Hold-out method.

Early stopping and polynomial smoothing in regression with reproducing kernels

In this paper we study the problem of early stopping for iterative learning algorithms in reproducing kernel Hilbert space (RKHS) in the nonparametric regression framework. In particular, we work with gradient descent and (iterative) kernel ridge regression algorithms. We present a data-driven rule to perform early stopping without a validation set that is based on the so-called minimum discrepancy principle. This method enjoys only one assumption on the regression function: it belongs to a reproducing kernel Hilbert space (RKHS). The proposed rule is proved to be minimax optimal over different types of kernel spaces, including finite rank and Sobolev smoothness classes. The proof is derived from the fixed-point analysis of the localized Rademacher complexities, which is a standard technique for obtaining optimal rates in the nonparametric regression literature. In addition to that, we present simulations results on artificial datasets that show comparable performance of the designed rule with respect to other stopping rules such as the one determined by V-fold cross-validation.