A Constant-per-Iteration Likelihood Ratio Test for Online Changepoint Detection for Exponential Family Models

Online changepoint detection algorithms that are based on likelihood-ratio tests have been shown to have excellent statistical properties. However, a simple online implementation is computationally infeasible as, at time $T$, it involves considering $O(T)$ possible locations for the change. Recently, the FOCuS algorithm has been introduced for detecting changes in mean in Gaussian data that decreases the per-iteration cost to $O(\log T)$. This is possible by using pruning ideas, which reduce the set of changepoint locations that need to be considered at time $T$ to approximately $\log T$. We show that if one wishes to perform the likelihood ratio test for a different one-parameter exponential family model, then exactly the same pruning rule can be used, and again one need only consider approximately $\log T$ locations at iteration $T$. Furthermore, we show how we can adaptively perform the maximisation step of the algorithm so that we need only maximise the test statistic over a small subset of these possible locations. Empirical results show that the resulting online algorithm, which can detect changes under a wide range of models, has a constant-per-iteration cost on average.

A Log-Linear Non-Parametric Online Changepoint Detection Algorithm based on Functional Pruning

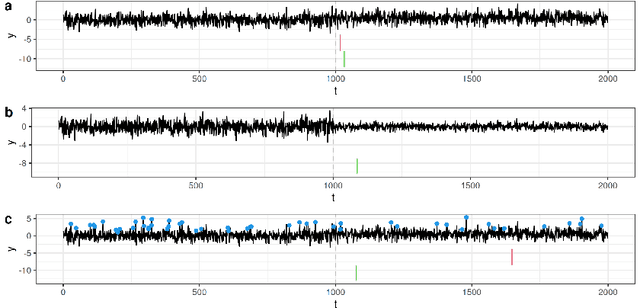
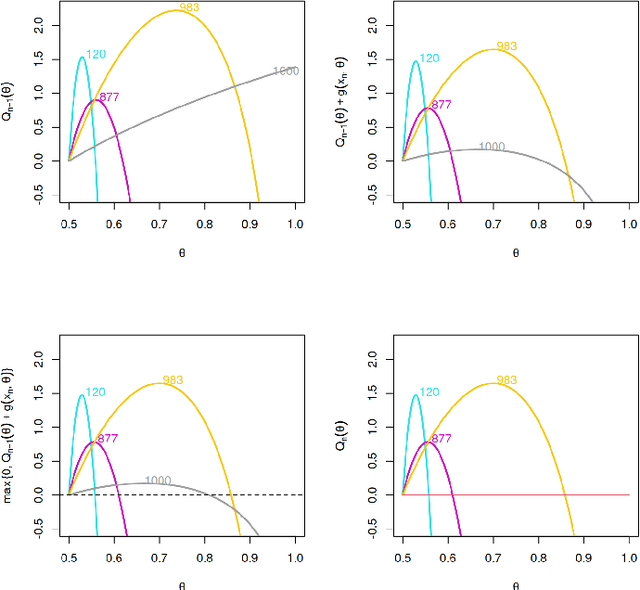
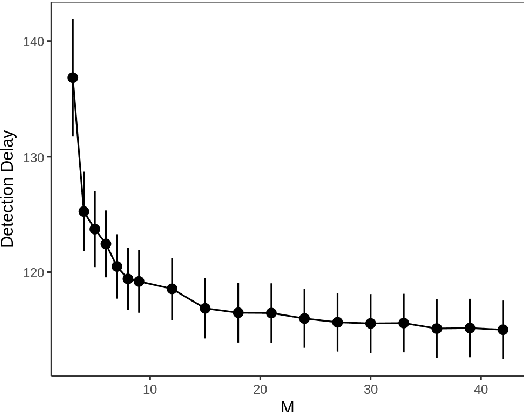
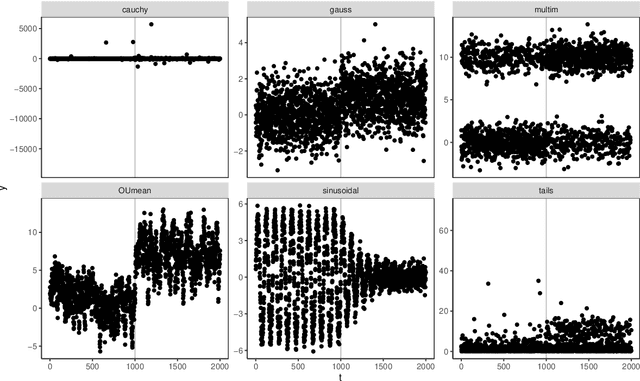
Online changepoint detection aims to detect anomalies and changes in real-time in high-frequency data streams, sometimes with limited available computational resources. This is an important task that is rooted in many real-world applications, including and not limited to cybersecurity, medicine and astrophysics. While fast and efficient online algorithms have been recently introduced, these rely on parametric assumptions which are often violated in practical applications. Motivated by data streams from the telecommunications sector, we build a flexible nonparametric approach to detect a change in the distribution of a sequence. Our procedure, NP-FOCuS, builds a sequential likelihood ratio test for a change in a set of points of the empirical cumulative density function of our data. This is achieved by keeping track of the number of observations above or below those points. Thanks to functional pruning ideas, NP-FOCuS has a computational cost that is log-linear in the number of observations and is suitable for high-frequency data streams. In terms of detection power, NP-FOCuS is seen to outperform current nonparametric online changepoint techniques in a variety of settings. We demonstrate the utility of the procedure on both simulated and real data.

Fast Online Changepoint Detection via Functional Pruning CUSUM statistics

Many modern applications of online changepoint detection require the ability to process high-frequency observations, sometimes with limited available computational resources. Online algorithms for detecting a change in mean often involve using a moving window, or specifying the expected size of change. Such choices affect which changes the algorithms have most power to detect. We introduce an algorithm, Functional Online CuSUM (FOCuS), which is equivalent to running these earlier methods simultaneously for all sizes of window, or all possible values for the size of change. Our theoretical results give tight bounds on the expected computational cost per iteration of FOCuS, with this being logarithmic in the number of observations. We show how FOCuS can be applied to a number of different change in mean scenarios, and demonstrate its practical utility through its state-of-the art performance at detecting anomalous behaviour in computer server data.