Stochastic Gradient Piecewise Deterministic Monte Carlo Samplers

Recent work has suggested using Monte Carlo methods based on piecewise deterministic Markov processes (PDMPs) to sample from target distributions of interest. PDMPs are non-reversible continuous-time processes endowed with momentum, and hence can mix better than standard reversible MCMC samplers. Furthermore, they can incorporate exact sub-sampling schemes which only require access to a single (randomly selected) data point at each iteration, yet without introducing bias to the algorithm's stationary distribution. However, the range of models for which PDMPs can be used, particularly with sub-sampling, is limited. We propose approximate simulation of PDMPs with sub-sampling for scalable sampling from posterior distributions. The approximation takes the form of an Euler approximation to the true PDMP dynamics, and involves using an estimate of the gradient of the log-posterior based on a data sub-sample. We thus call this class of algorithms stochastic-gradient PDMPs. Importantly, the trajectories of stochastic-gradient PDMPs are continuous and can leverage recent ideas for sampling from measures with continuous and atomic components. We show these methods are easy to implement, present results on their approximation error and demonstrate numerically that this class of algorithms has similar efficiency to, but is more robust than, stochastic gradient Langevin dynamics.

The Boomerang Sampler

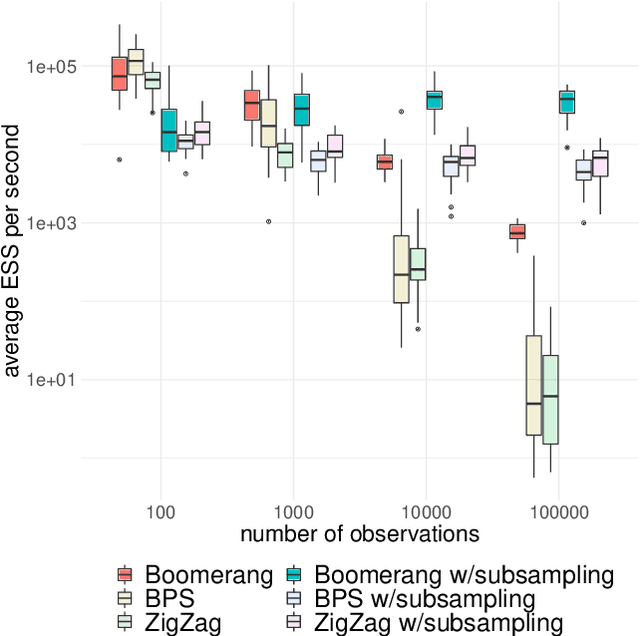
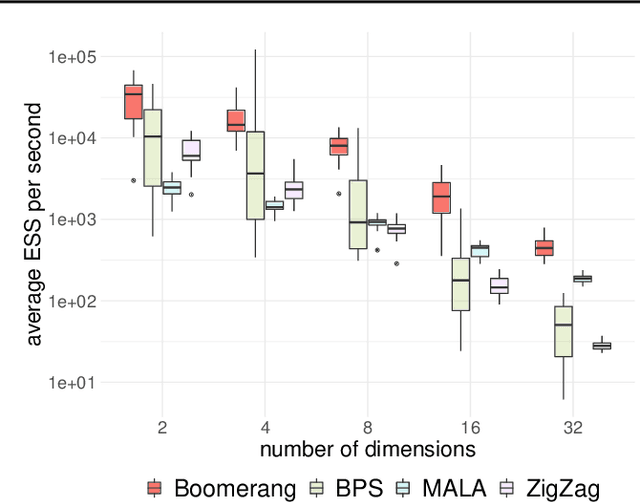
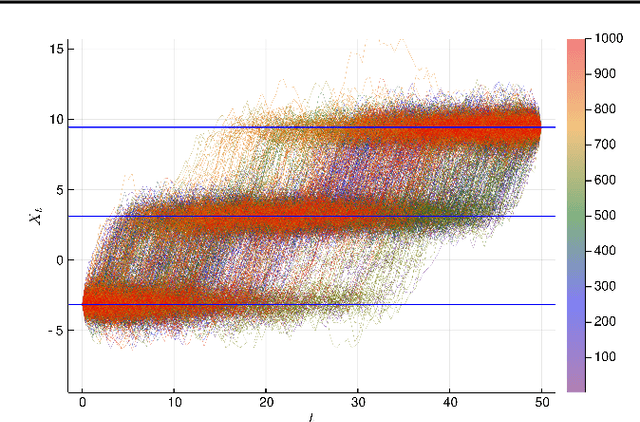
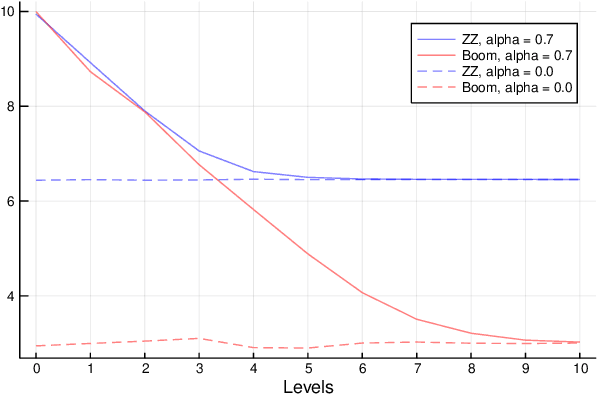
This paper introduces the boomerang sampler as a novel class of continuous-time non-reversible Markov chain Monte Carlo algorithms. The methodology begins by representing the target density as a density, $e^{-U}$, with respect to a prescribed (usually) Gaussian measure and constructs a continuous trajectory consisting of a piecewise elliptical path. The method moves from one elliptical orbit to another according to a rate function which can be written in terms of $U$. We demonstrate that the method is easy to implement and demonstrate empirically that it can out-perform existing benchmark piecewise deterministic Markov processes such as the bouncy particle sampler and the Zig-Zag. In the Bayesian statistics context, these competitor algorithms are of substantial interest in the large data context due to the fact that they can adopt data subsampling techniques which are exact (ie induce no error in the stationary distribution). We demonstrate theoretically and empirically that we can also construct a control-variate subsampling boomerang sampler which is also exact, and which possesses remarkable scaling properties in the large data limit. We furthermore illustrate a factorised version on the simulation of diffusion bridges.