Integration of Active Learning and MCMC Sampling for Efficient Bayesian Calibration of Mechanical Properties

Recent advancements in Markov chain Monte Carlo (MCMC) sampling and surrogate modelling have significantly enhanced the feasibility of Bayesian analysis across engineering fields. However, the selection and integration of surrogate models and cutting-edge MCMC algorithms, often depend on ad-hoc decisions. A systematic assessment of their combined influence on analytical accuracy and efficiency is notably lacking. The present work offers a comprehensive comparative study, employing a scalable case study in computational mechanics focused on the inference of spatially varying material parameters, that sheds light on the impact of methodological choices for surrogate modelling and sampling. We show that a priori training of the surrogate model introduces large errors in the posterior estimation even in low to moderate dimensions. We introduce a simple active learning strategy based on the path of the MCMC algorithm that is superior to all a priori trained models, and determine its training data requirements. We demonstrate that the choice of the MCMC algorithm has only a small influence on the amount of training data but no significant influence on the accuracy of the resulting surrogate model. Further, we show that the accuracy of the posterior estimation largely depends on the surrogate model, but not even a tailored surrogate guarantees convergence of the MCMC.Finally, we identify the forward model as the bottleneck in the inference process, not the MCMC algorithm. While related works focus on employing advanced MCMC algorithms, we demonstrate that the training data requirements render the surrogate modelling approach infeasible before the benefits of these gradient-based MCMC algorithms on cheap models can be reaped.

The Boomerang Sampler

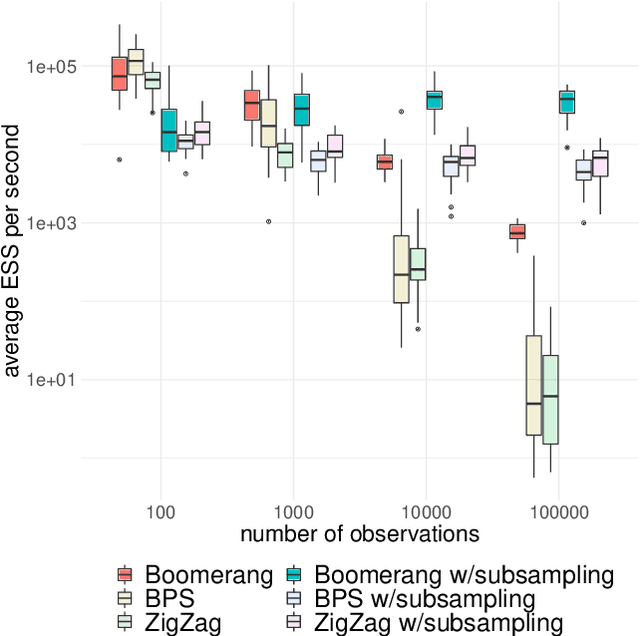
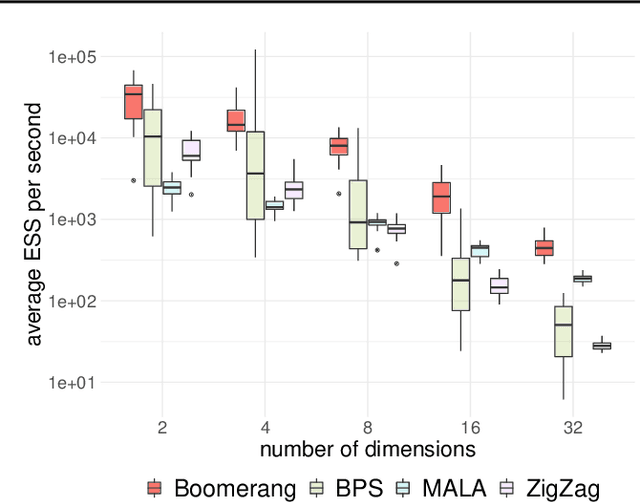
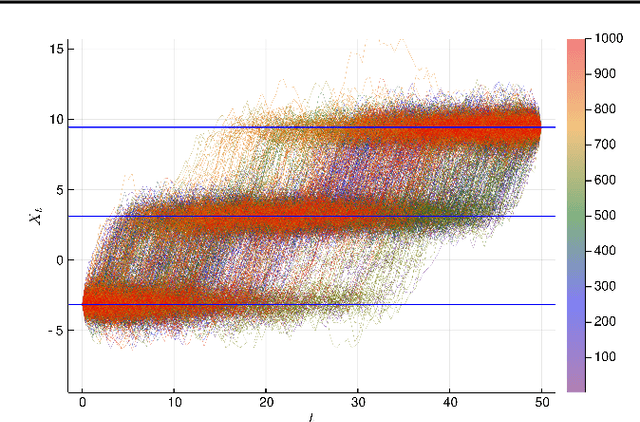
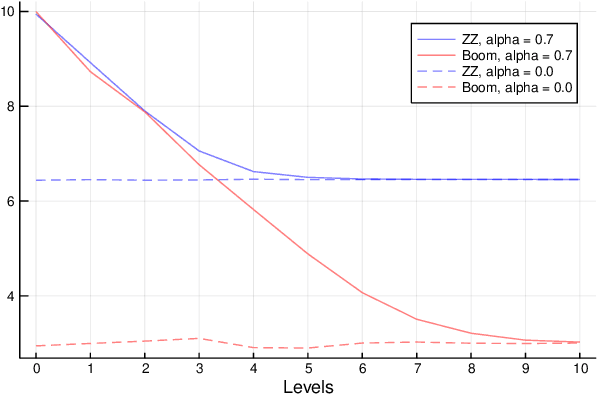
This paper introduces the boomerang sampler as a novel class of continuous-time non-reversible Markov chain Monte Carlo algorithms. The methodology begins by representing the target density as a density, $e^{-U}$, with respect to a prescribed (usually) Gaussian measure and constructs a continuous trajectory consisting of a piecewise elliptical path. The method moves from one elliptical orbit to another according to a rate function which can be written in terms of $U$. We demonstrate that the method is easy to implement and demonstrate empirically that it can out-perform existing benchmark piecewise deterministic Markov processes such as the bouncy particle sampler and the Zig-Zag. In the Bayesian statistics context, these competitor algorithms are of substantial interest in the large data context due to the fact that they can adopt data subsampling techniques which are exact (ie induce no error in the stationary distribution). We demonstrate theoretically and empirically that we can also construct a control-variate subsampling boomerang sampler which is also exact, and which possesses remarkable scaling properties in the large data limit. We furthermore illustrate a factorised version on the simulation of diffusion bridges.

Piecewise Deterministic Markov Processes for Continuous-Time Monte Carlo

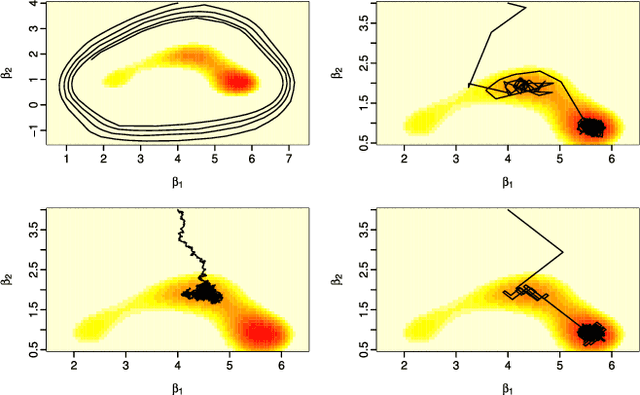
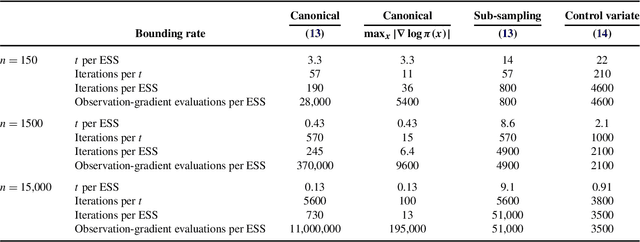
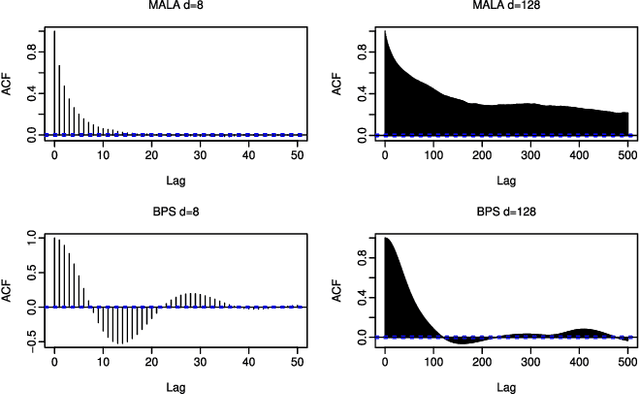
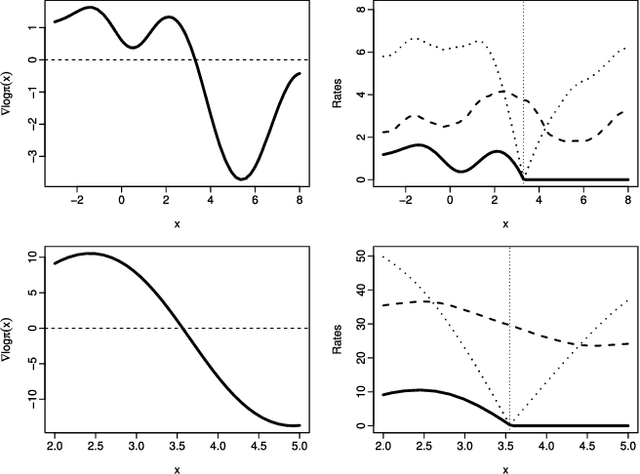
Recently there have been exciting developments in Monte Carlo methods, with the development of new MCMC and sequential Monte Carlo (SMC) algorithms which are based on continuous-time, rather than discrete-time, Markov processes. This has led to some fundamentally new Monte Carlo algorithms which can be used to sample from, say, a posterior distribution. Interestingly, continuous-time algorithms seem particularly well suited to Bayesian analysis in big-data settings as they need only access a small sub-set of data points at each iteration, and yet are still guaranteed to target the true posterior distribution. Whilst continuous-time MCMC and SMC methods have been developed independently we show here that they are related by the fact that both involve simulating a piecewise deterministic Markov process. Furthermore we show that the methods developed to date are just specific cases of a potentially much wider class of continuous-time Monte Carlo algorithms. We give an informal introduction to piecewise deterministic Markov processes, covering the aspects relevant to these new Monte Carlo algorithms, with a view to making the development of new continuous-time Monte Carlo more accessible. We focus on how and why sub-sampling ideas can be used with these algorithms, and aim to give insight into how these new algorithms can be implemented, and what are some of the issues that affect their efficiency.

KL-learning: Online solution of Kullback-Leibler control problems

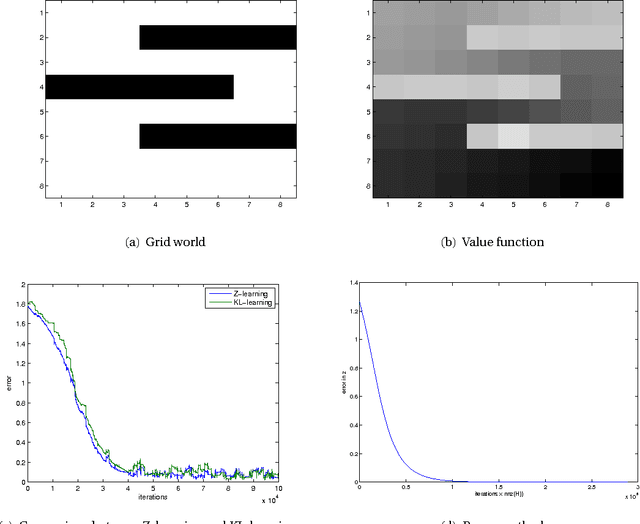
We introduce a stochastic approximation method for the solution of an ergodic Kullback-Leibler control problem. A Kullback-Leibler control problem is a Markov decision process on a finite state space in which the control cost is proportional to a Kullback-Leibler divergence of the controlled transition probabilities with respect to the uncontrolled transition probabilities. The algorithm discussed in this work allows for a sound theoretical analysis using the ODE method. In a numerical experiment the algorithm is shown to be comparable to the power method and the related Z-learning algorithm in terms of convergence speed. It may be used as the basis of a reinforcement learning style algorithm for Markov decision problems.