On the Sample Complexity of Reinforcement Learning with a Generative Model

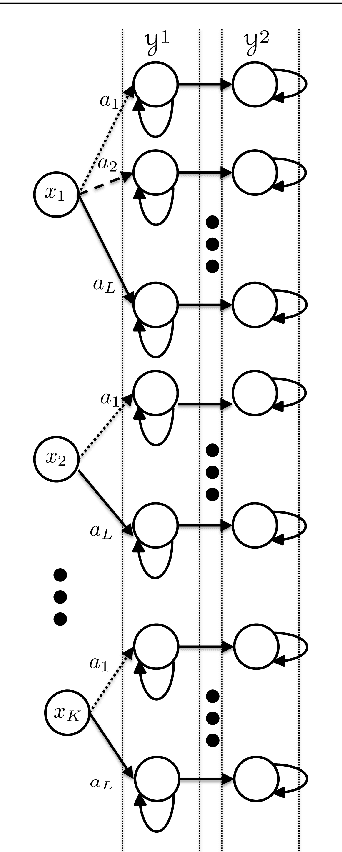
We consider the problem of learning the optimal action-value function in the discounted-reward Markov decision processes (MDPs). We prove a new PAC bound on the sample-complexity of model-based value iteration algorithm in the presence of the generative model, which indicates that for an MDP with N state-action pairs and the discount factor \gamma\in[0,1) only O(N\log(N/\delta)/((1-\gamma)^3\epsilon^2)) samples are required to find an \epsilon-optimal estimation of the action-value function with the probability 1-\delta. We also prove a matching lower bound of \Theta (N\log(N/\delta)/((1-\gamma)^3\epsilon^2)) on the sample complexity of estimating the optimal action-value function by every RL algorithm. To the best of our knowledge, this is the first matching result on the sample complexity of estimating the optimal (action-) value function in which the upper bound matches the lower bound of RL in terms of N, \epsilon, \delta and 1/(1-\gamma). Also, both our lower bound and our upper bound significantly improve on the state-of-the-art in terms of 1/(1-\gamma).

KL-learning: Online solution of Kullback-Leibler control problems

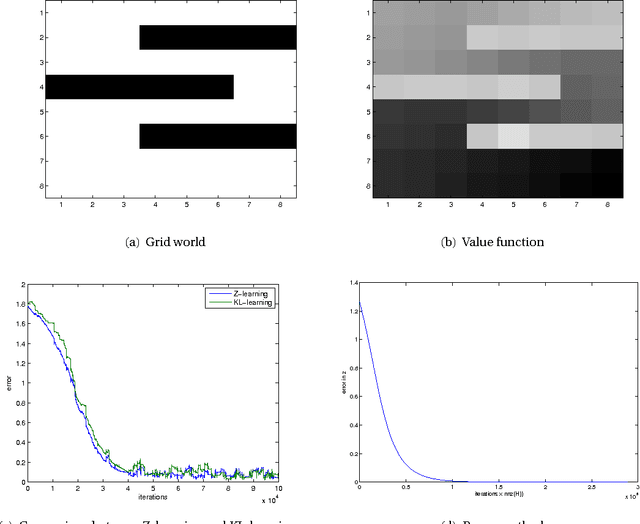
We introduce a stochastic approximation method for the solution of an ergodic Kullback-Leibler control problem. A Kullback-Leibler control problem is a Markov decision process on a finite state space in which the control cost is proportional to a Kullback-Leibler divergence of the controlled transition probabilities with respect to the uncontrolled transition probabilities. The algorithm discussed in this work allows for a sound theoretical analysis using the ODE method. In a numerical experiment the algorithm is shown to be comparable to the power method and the related Z-learning algorithm in terms of convergence speed. It may be used as the basis of a reinforcement learning style algorithm for Markov decision problems.

Loop corrections for message passing algorithms in continuous variable models

In this paper we derive the equations for Loop Corrected Belief Propagation on a continuous variable Gaussian model. Using the exactness of the averages for belief propagation for Gaussian models, a different way of obtaining the covariances is found, based on Belief Propagation on cavity graphs. We discuss the relation of this loop correction algorithm to Expectation Propagation algorithms for the case in which the model is no longer Gaussian, but slightly perturbed by nonlinear terms.

Loop corrections for approximate inference

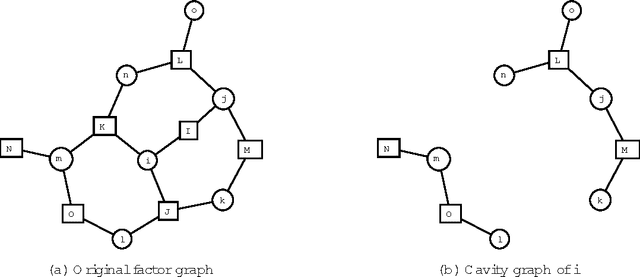
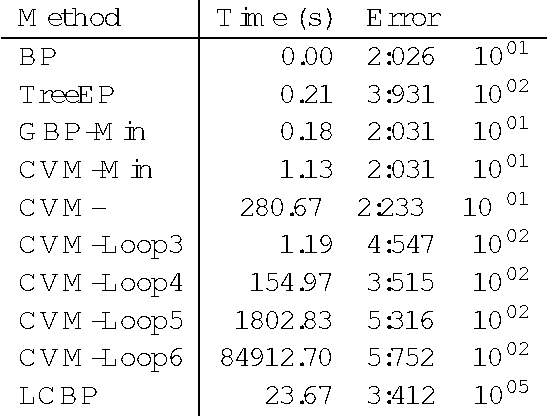
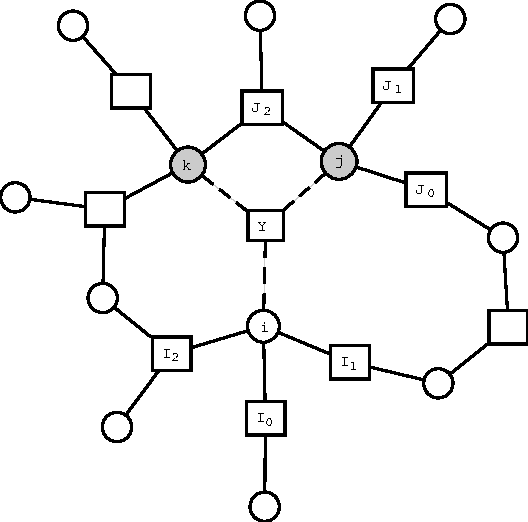
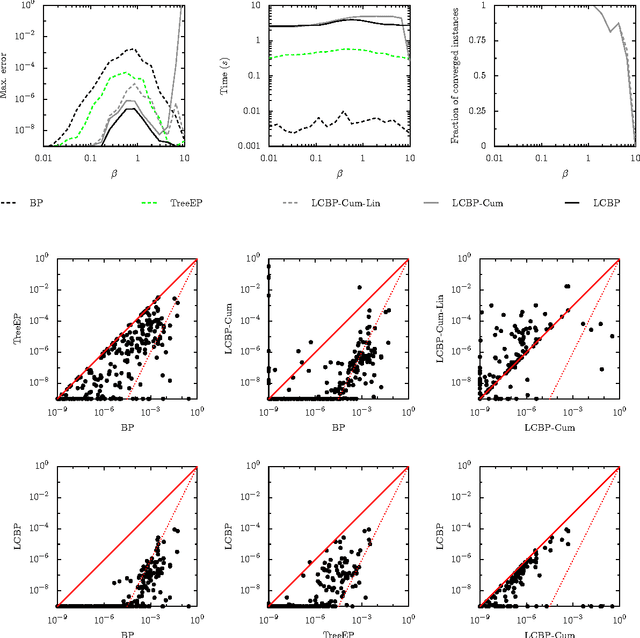
We propose a method for improving approximate inference methods that corrects for the influence of loops in the graphical model. The method is applicable to arbitrary factor graphs, provided that the size of the Markov blankets is not too large. It is an alternative implementation of an idea introduced recently by Montanari and Rizzo (2005). In its simplest form, which amounts to the assumption that no loops are present, the method reduces to the minimal Cluster Variation Method approximation (which uses maximal factors as outer clusters). On the other hand, using estimates of the effect of loops (obtained by some approximate inference algorithm) and applying the Loop Correcting (LC) method usually gives significantly better results than applying the approximate inference algorithm directly without loop corrections. Indeed, we often observe that the loop corrected error is approximately the square of the error of the approximate inference method used to estimate the effect of loops. We compare different variants of the Loop Correcting method with other approximate inference methods on a variety of graphical models, including "real world" networks, and conclude that the LC approach generally obtains the most accurate results.