Central Limit Theorem for ergodic averages of Markov chains \& the comparison of sampling algorithms for heavy-tailed distributions

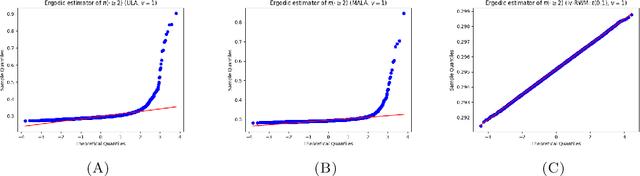
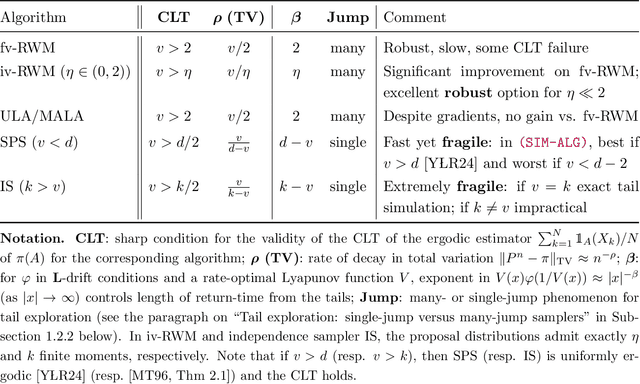
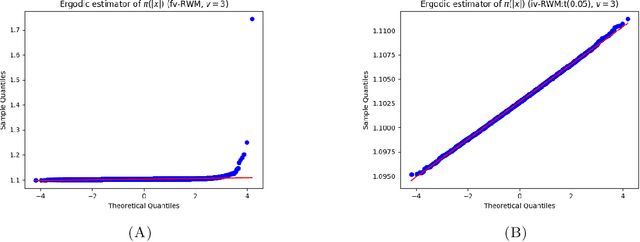
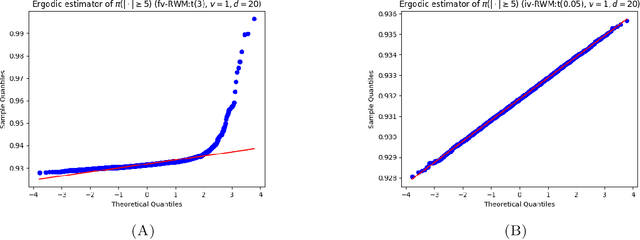
Establishing central limit theorems (CLTs) for ergodic averages of Markov chains is a fundamental problem in probability and its applications. Since the seminal work~\cite{MR834478}, a vast literature has emerged on the sufficient conditions for such CLTs. To counterbalance this, the present paper provides verifiable necessary conditions for CLTs of ergodic averages of Markov chains on general state spaces. Our theory is based on drift conditions, which also yield lower bounds on the rates of convergence to stationarity in various metrics. The validity of the ergodic CLT is of particular importance for sampling algorithms, where it underpins the error analysis of estimators in Bayesian statistics and machine learning. Although heavy-tailed sampling is of central importance in applications, the characterisation of the CLT and the convergence rates are theoretically poorly understood for almost all practically-used Markov chain Monte Carlo (MCMC) algorithms. In this setting our results provide sharp conditions on the validity of the ergodic CLT and establish convergence rates for large families of MCMC sampling algorithms for heavy-tailed targets. Our study includes a rather complete analyses for random walk Metropolis samplers (with finite- and infinite-variance proposals), Metropolis-adjusted and unadjusted Langevin algorithms and the stereographic projection sampler (as well as the independence sampler). By providing these sharp results via our practical drift conditions, our theory offers significant insights into the problems of algorithm selection and comparison for sampling heavy-tailed distributions (see short YouTube presentations~\cite{YouTube_talk} describing our \href{https://youtu.be/m2y7U4cEqy4}{\underline{theory}} and \href{https://youtu.be/w8I_oOweuko}{\underline{applications}}).

The Boomerang Sampler

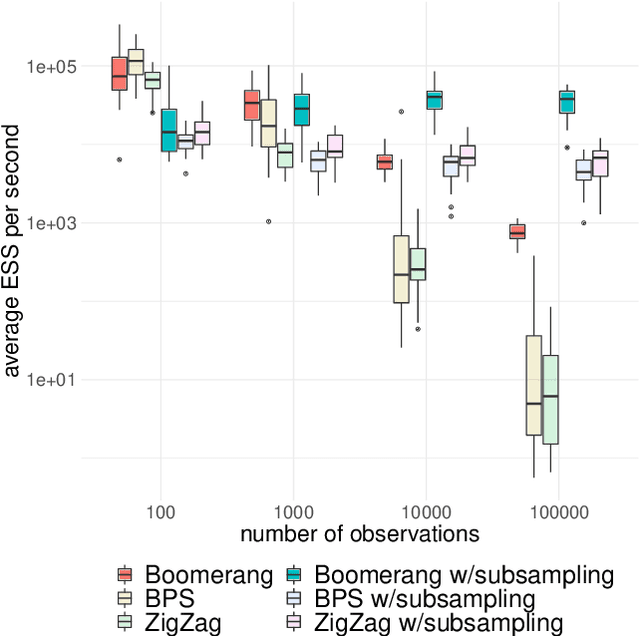
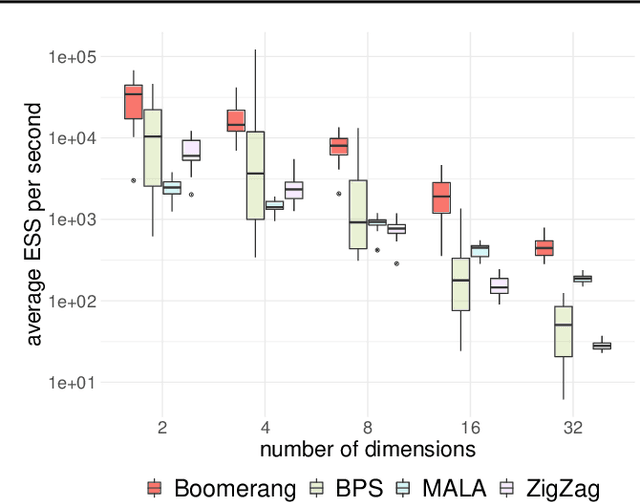
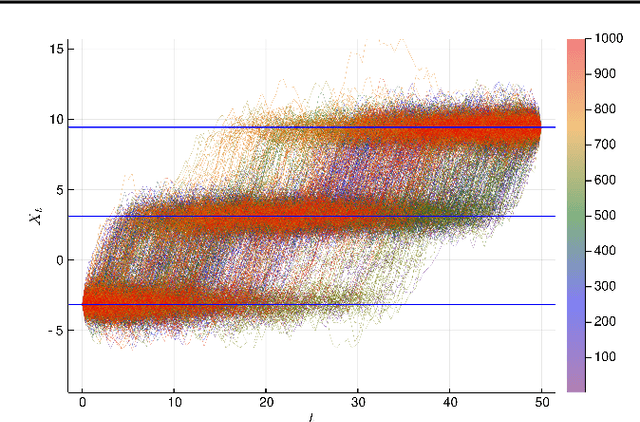
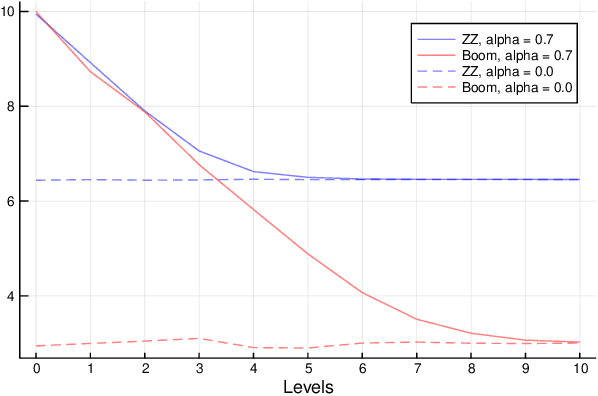
This paper introduces the boomerang sampler as a novel class of continuous-time non-reversible Markov chain Monte Carlo algorithms. The methodology begins by representing the target density as a density, $e^{-U}$, with respect to a prescribed (usually) Gaussian measure and constructs a continuous trajectory consisting of a piecewise elliptical path. The method moves from one elliptical orbit to another according to a rate function which can be written in terms of $U$. We demonstrate that the method is easy to implement and demonstrate empirically that it can out-perform existing benchmark piecewise deterministic Markov processes such as the bouncy particle sampler and the Zig-Zag. In the Bayesian statistics context, these competitor algorithms are of substantial interest in the large data context due to the fact that they can adopt data subsampling techniques which are exact (ie induce no error in the stationary distribution). We demonstrate theoretically and empirically that we can also construct a control-variate subsampling boomerang sampler which is also exact, and which possesses remarkable scaling properties in the large data limit. We furthermore illustrate a factorised version on the simulation of diffusion bridges.

Scalable Importance Tempering and Bayesian Variable Selection

We propose a Monte Carlo algorithm to sample from high-dimensional probability distributions that combines Markov chain Monte Carlo (MCMC) and importance sampling. We provide a careful theoretical analysis, including guarantees on robustness to high-dimensionality, explicit comparison with standard MCMC and illustrations of the potential improvements in efficiency. Simple and concrete intuition is provided for when the novel scheme is expected to outperform standard schemes. When applied to Bayesian Variable Selection problems, the novel algorithm is orders of magnitude more efficient than available alternative sampling schemes and allows to perform fast and reliable fully Bayesian inferences with tens of thousands regressors.