Divide-and-Conquer Monte Carlo Fusion

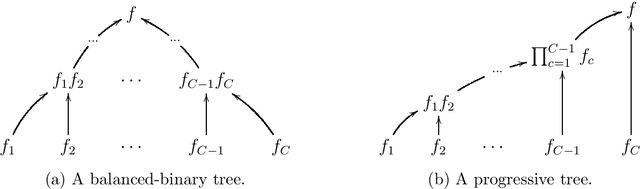
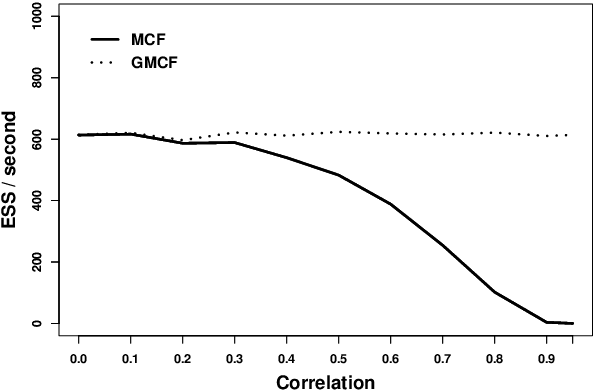
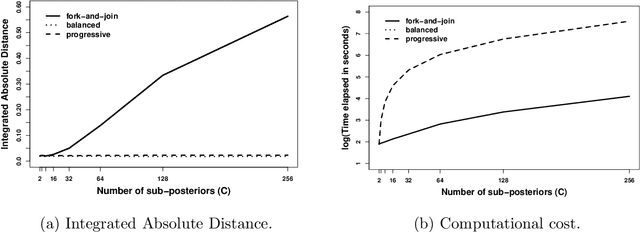
Combining several (sample approximations of) distributions, which we term sub-posteriors, into a single distribution proportional to their product, is a common challenge. For instance, in distributed `big data' problems, or when working under multi-party privacy constraints. Many existing approaches resort to approximating the individual sub-posteriors for practical necessity, then representing the resulting approximate posterior. The quality of the posterior approximation for these approaches is poor when the sub-posteriors fall out-with a narrow range of distributional form. Recently, a Fusion approach has been proposed which finds a direct and exact Monte Carlo approximation of the posterior (as opposed to the sub-posteriors), circumventing the drawbacks of approximate approaches. Unfortunately, existing Fusion approaches have a number of computational limitations, particularly when unifying a large number of sub-posteriors. In this paper, we generalise the theory underpinning existing Fusion approaches, and embed the resulting methodology within a recursive divide-and-conquer sequential Monte Carlo paradigm. This ultimately leads to a competitive Fusion approach, which is robust to increasing numbers of sub-posteriors.

Piecewise Deterministic Markov Processes for Continuous-Time Monte Carlo

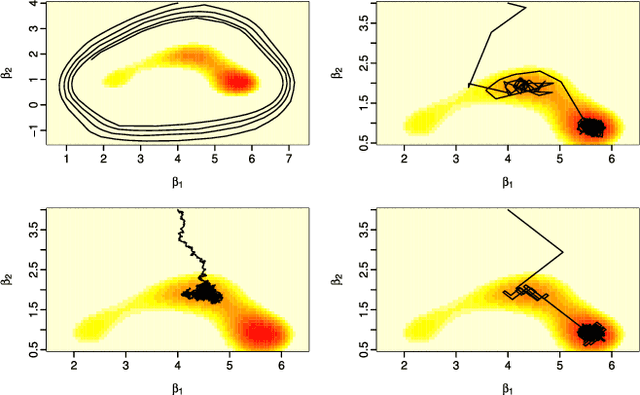
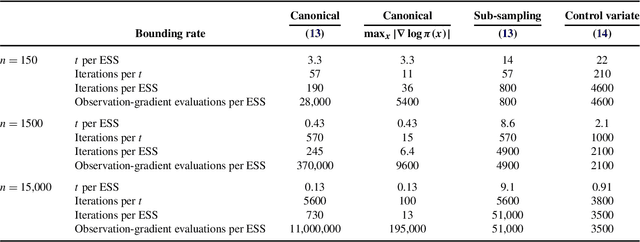
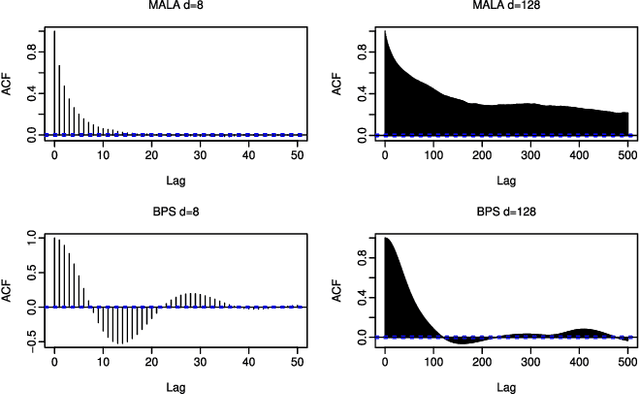
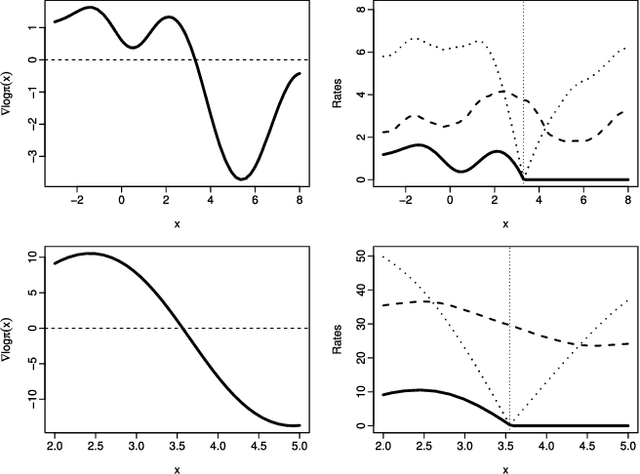
Recently there have been exciting developments in Monte Carlo methods, with the development of new MCMC and sequential Monte Carlo (SMC) algorithms which are based on continuous-time, rather than discrete-time, Markov processes. This has led to some fundamentally new Monte Carlo algorithms which can be used to sample from, say, a posterior distribution. Interestingly, continuous-time algorithms seem particularly well suited to Bayesian analysis in big-data settings as they need only access a small sub-set of data points at each iteration, and yet are still guaranteed to target the true posterior distribution. Whilst continuous-time MCMC and SMC methods have been developed independently we show here that they are related by the fact that both involve simulating a piecewise deterministic Markov process. Furthermore we show that the methods developed to date are just specific cases of a potentially much wider class of continuous-time Monte Carlo algorithms. We give an informal introduction to piecewise deterministic Markov processes, covering the aspects relevant to these new Monte Carlo algorithms, with a view to making the development of new continuous-time Monte Carlo more accessible. We focus on how and why sub-sampling ideas can be used with these algorithms, and aim to give insight into how these new algorithms can be implemented, and what are some of the issues that affect their efficiency.