Adaptively Truncating Backpropagation Through Time to Control Gradient Bias

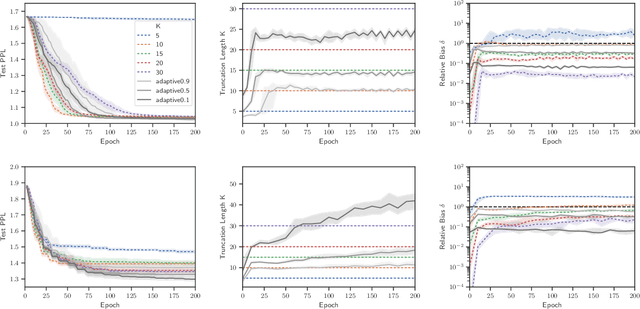
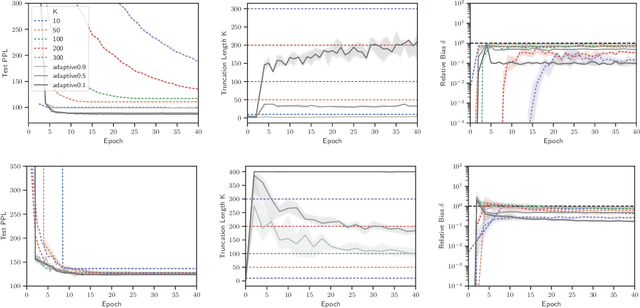
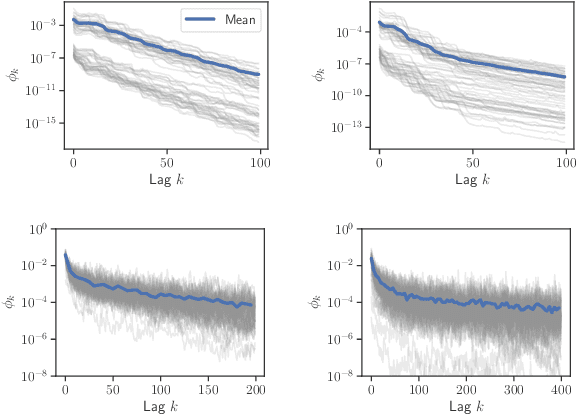
Truncated backpropagation through time (TBPTT) is a popular method for learning in recurrent neural networks (RNNs) that saves computation and memory at the cost of bias by truncating backpropagation after a fixed number of lags. In practice, choosing the optimal truncation length is difficult: TBPTT will not converge if the truncation length is too small, or will converge slowly if it is too large. We propose an adaptive TBPTT scheme that converts the problem from choosing a temporal lag to one of choosing a tolerable amount of gradient bias. For many realistic RNNs, the TBPTT gradients decay geometrically for large lags; under this condition, we can control the bias by varying the truncation length adaptively. For RNNs with smooth activation functions, we prove that this bias controls the convergence rate of SGD with biased gradients for our non-convex loss. Using this theory, we develop a practical method for adaptively estimating the truncation length during training. We evaluate our adaptive TBPTT method on synthetic data and language modeling tasks and find that our adaptive TBPTT ameliorates the computational pitfalls of fixed TBPTT.