Guillaume W. Basse
Model-assisted design of experiments in the presence of network correlated outcomes
May 18, 2017
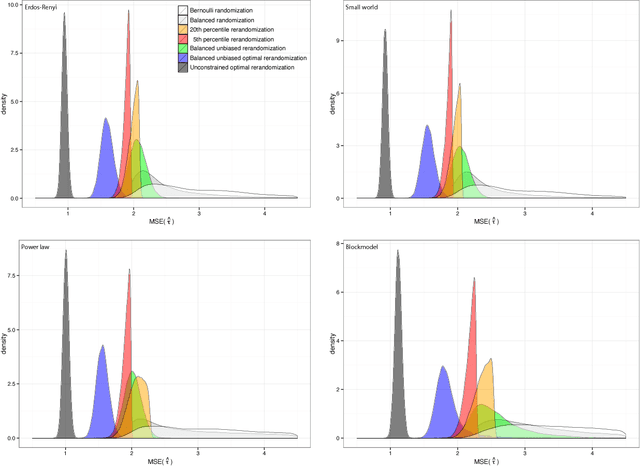
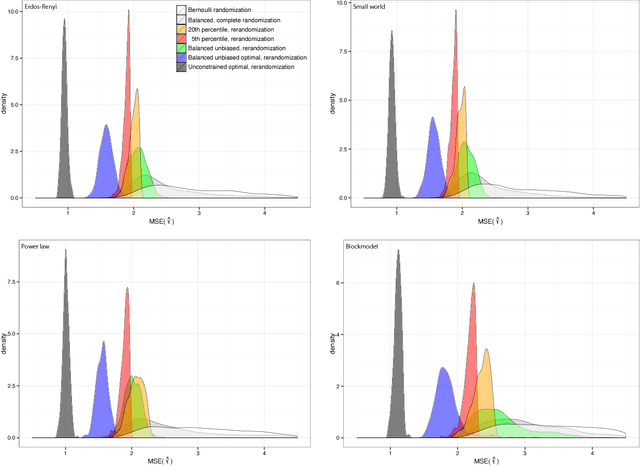
Abstract:We consider the problem of how to assign treatment in a randomized experiment, in which the correlation among the outcomes is informed by a network available pre-intervention. Working within the potential outcome causal framework, we develop a class of models that posit such a correlation structure among the outcomes. Then we leverage these models to develop restricted randomization strategies for allocating treatment optimally, by minimizing the mean square error of the estimated average treatment effect. Analytical decompositions of the mean square error, due both to the model and to the randomization distribution, provide insights into aspects of the optimal designs. In particular, the analysis suggests new notions of balance based on specific network quantities, in addition to classical covariate balance. The resulting balanced, optimal restricted randomization strategies are still design unbiased, in situations where the model used to derive them does not hold. We illustrate how the proposed treatment allocation strategies improve on allocations that ignore the network structure, with extensive simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge