Geometric Representations of Random Hypergraphs
Paper and Code
Apr 12, 2015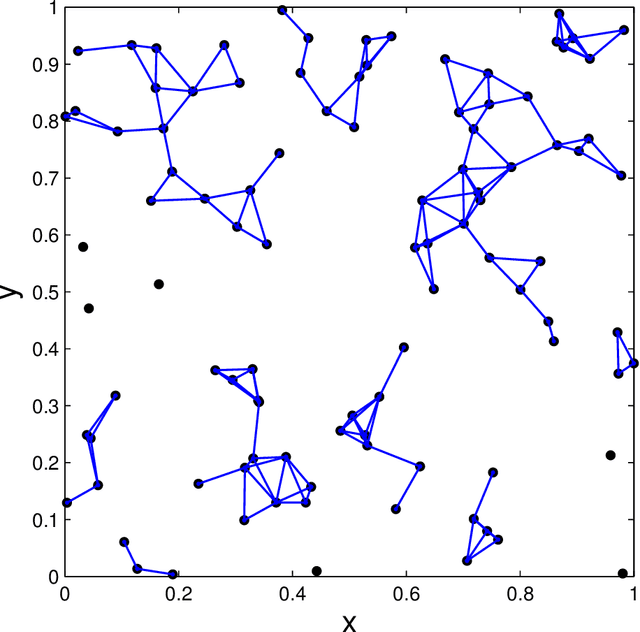

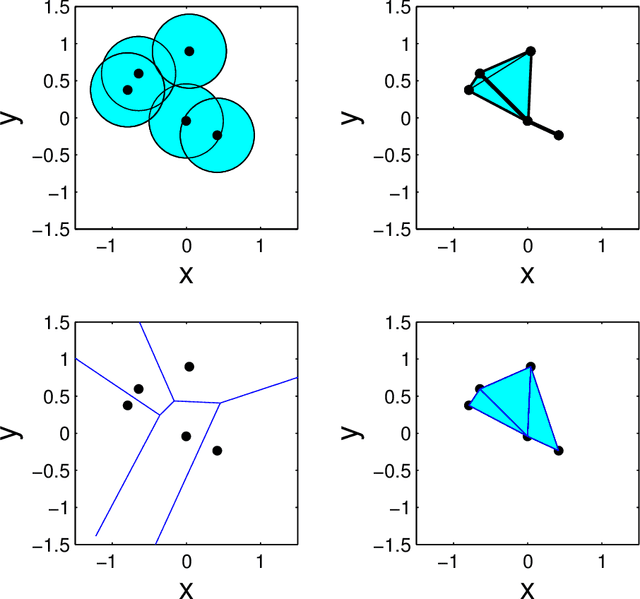
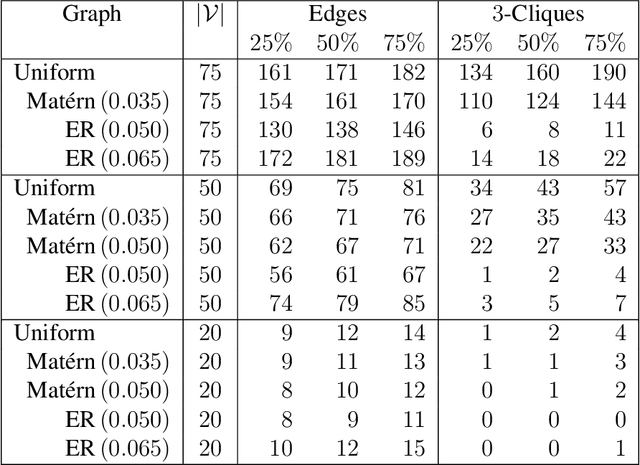
A parametrization of hypergraphs based on the geometry of points in $\mathbf{R}^d$ is developed. Informative prior distributions on hypergraphs are induced through this parametrization by priors on point configurations via spatial processes. This prior specification is used to infer conditional independence models or Markov structure of multivariate distributions. Specifically, we can recover both the junction tree factorization as well as the hyper Markov law. This approach offers greater control on the distribution of graph features than Erd\"os-R\'enyi random graphs, supports inference of factorizations that cannot be retrieved by a graph alone, and leads to new Metropolis\slash Hastings Markov chain Monte Carlo algorithms with both local and global moves in graph space. We illustrate the utility of this parametrization and prior specification using simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge