Copula variational inference
Paper and Code
Oct 31, 2015
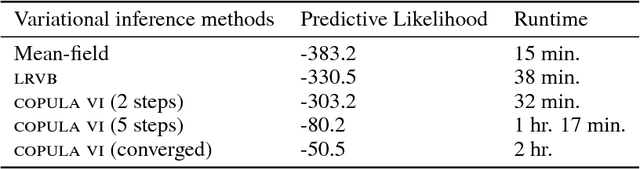
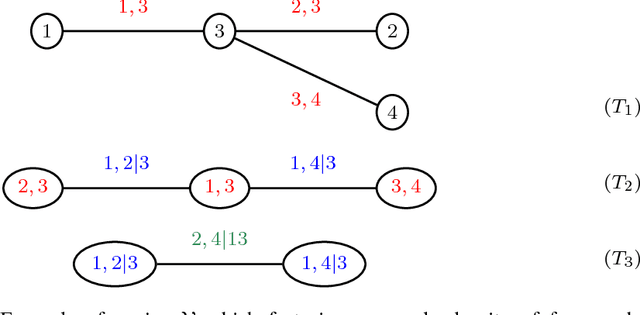
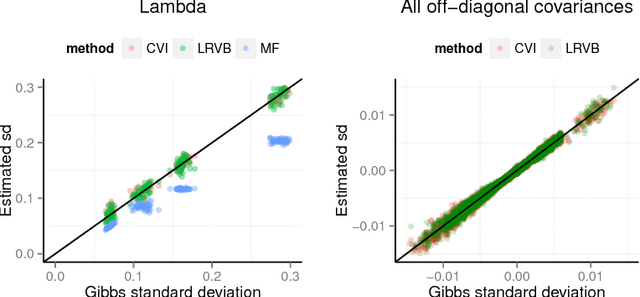
We develop a general variational inference method that preserves dependency among the latent variables. Our method uses copulas to augment the families of distributions used in mean-field and structured approximations. Copulas model the dependency that is not captured by the original variational distribution, and thus the augmented variational family guarantees better approximations to the posterior. With stochastic optimization, inference on the augmented distribution is scalable. Furthermore, our strategy is generic: it can be applied to any inference procedure that currently uses the mean-field or structured approach. Copula variational inference has many advantages: it reduces bias; it is less sensitive to local optima; it is less sensitive to hyperparameters; and it helps characterize and interpret the dependency among the latent variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge