Optimal Bounds between $f$-Divergences and Integral Probability Metrics

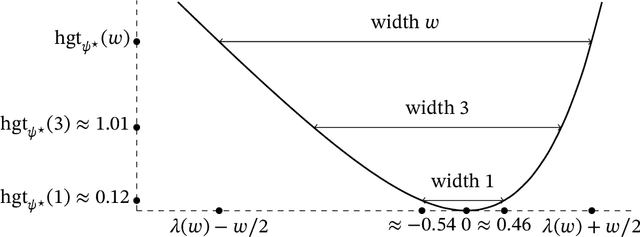
The families of $f$-divergences (e.g. the Kullback-Leibler divergence) and Integral Probability Metrics (e.g. total variation distance or maximum mean discrepancies) are commonly used in optimization and estimation. In this work, we systematically study the relationship between these two families from the perspective of convex duality. Starting from a tight variational representation of the $f$-divergence, we derive a generalization of the moment generating function, which we show exactly characterizes the best lower bound of the $f$-divergence as a function of a given IPM. Using this characterization, we obtain new bounds on IPMs defined by classes of unbounded functions, while also recovering in a unified manner well-known results for bounded and subgaussian functions (e.g. Pinsker's inequality and Hoeffding's lemma). The variational representation also allows us to prove new results on the topological properties of the divergence which may be of independent interest.

Morph: Flexible Acceleration for 3D CNN-based Video Understanding

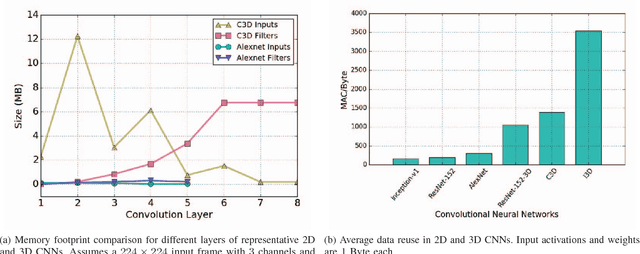
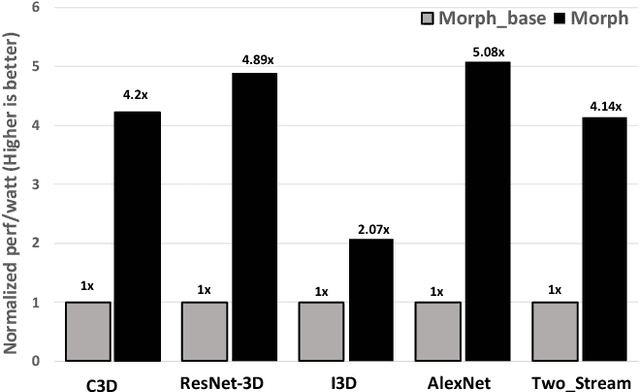
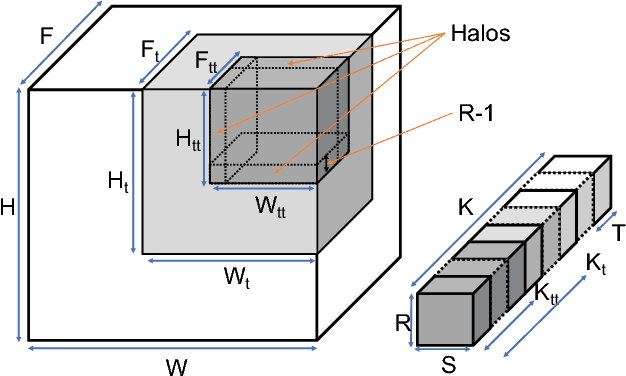
The past several years have seen both an explosion in the use of Convolutional Neural Networks (CNNs) and the design of accelerators to make CNN inference practical. In the architecture community, the lion share of effort has targeted CNN inference for image recognition. The closely related problem of video recognition has received far less attention as an accelerator target. This is surprising, as video recognition is more computationally intensive than image recognition, and video traffic is predicted to be the majority of internet traffic in the coming years. This paper fills the gap between algorithmic and hardware advances for video recognition by providing a design space exploration and flexible architecture for accelerating 3D Convolutional Neural Networks (3D CNNs) - the core kernel in modern video understanding. When compared to (2D) CNNs used for image recognition, efficiently accelerating 3D CNNs poses a significant engineering challenge due to their large (and variable over time) memory footprint and higher dimensionality. To address these challenges, we design a novel accelerator, called Morph, that can adaptively support different spatial and temporal tiling strategies depending on the needs of each layer of each target 3D CNN. We codesign a software infrastructure alongside the Morph hardware to find good-fit parameters to control the hardware. Evaluated on state-of-the-art 3D CNNs, Morph achieves up to 3.4x (2.5x average) reduction in energy consumption and improves performance/watt by up to 5.1x (4x average) compared to a baseline 3D CNN accelerator, with an area overhead of 5%. Morph further achieves a 15.9x average energy reduction on 3D CNNs when compared to Eyeriss.

UCNN: Exploiting Computational Reuse in Deep Neural Networks via Weight Repetition

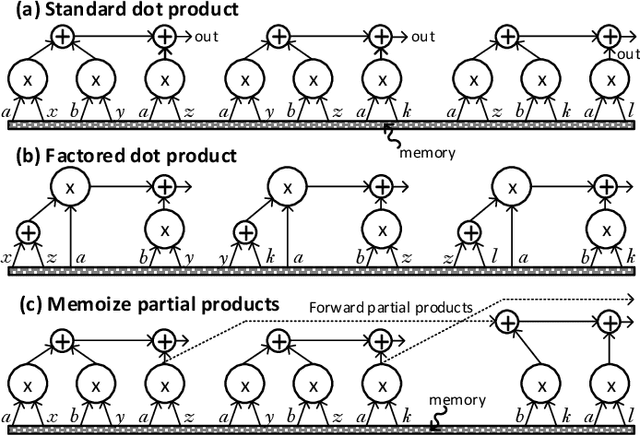
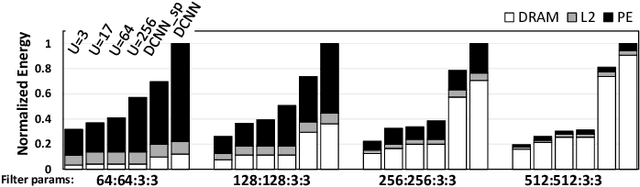
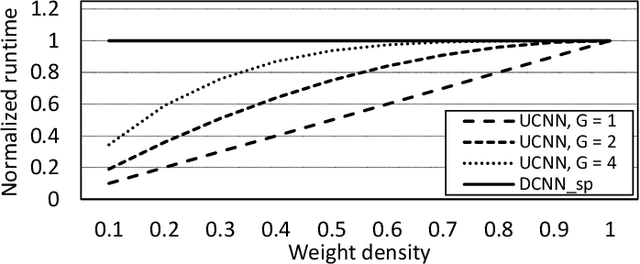
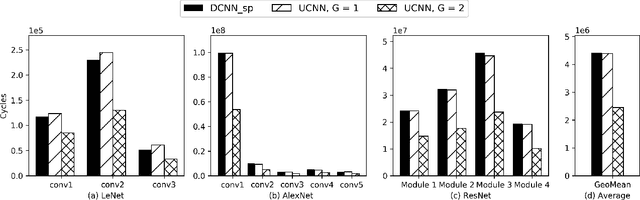
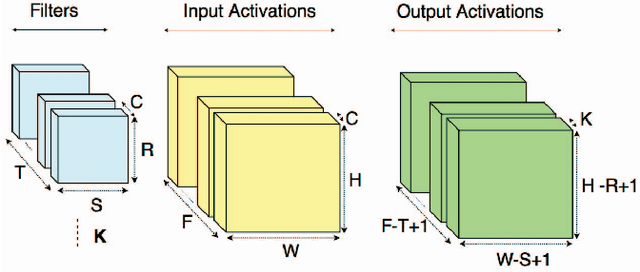
Convolutional Neural Networks (CNNs) have begun to permeate all corners of electronic society (from voice recognition to scene generation) due to their high accuracy and machine efficiency per operation. At their core, CNN computations are made up of multi-dimensional dot products between weight and input vectors. This paper studies how weight repetition ---when the same weight occurs multiple times in or across weight vectors--- can be exploited to save energy and improve performance during CNN inference. This generalizes a popular line of work to improve efficiency from CNN weight sparsity, as reducing computation due to repeated zero weights is a special case of reducing computation due to repeated weights. To exploit weight repetition, this paper proposes a new CNN accelerator called the Unique Weight CNN Accelerator (UCNN). UCNN uses weight repetition to reuse CNN sub-computations (e.g., dot products) and to reduce CNN model size when stored in off-chip DRAM ---both of which save energy. UCNN further improves performance by exploiting sparsity in weights. We evaluate UCNN with an accelerator-level cycle and energy model and with an RTL implementation of the UCNN processing element. On three contemporary CNNs, UCNN improves throughput-normalized energy consumption by 1.2x - 4x, relative to a similarly provisioned baseline accelerator that uses Eyeriss-style sparsity optimizations. At the same time, the UCNN processing element adds only 17-24% area overhead relative to the same baseline.