ABCinML: Anticipatory Bias Correction in Machine Learning Applications

The idealization of a static machine-learned model, trained once and deployed forever, is not practical. As input distributions change over time, the model will not only lose accuracy, any constraints to reduce bias against a protected class may fail to work as intended. Thus, researchers have begun to explore ways to maintain algorithmic fairness over time. One line of work focuses on dynamic learning: retraining after each batch, and the other on robust learning which tries to make algorithms robust against all possible future changes. Dynamic learning seeks to reduce biases soon after they have occurred and robust learning often yields (overly) conservative models. We propose an anticipatory dynamic learning approach for correcting the algorithm to mitigate bias before it occurs. Specifically, we make use of anticipations regarding the relative distributions of population subgroups (e.g., relative ratios of male and female applicants) in the next cycle to identify the right parameters for an importance weighing fairness approach. Results from experiments over multiple real-world datasets suggest that this approach has promise for anticipatory bias correction.

No-Regret and Incentive-Compatible Online Learning

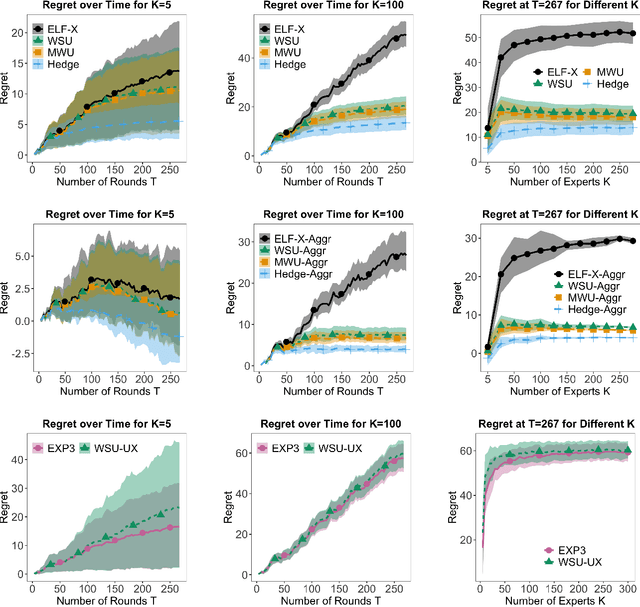
We study online learning settings in which experts act strategically to maximize their influence on the learning algorithm's predictions by potentially misreporting their beliefs about a sequence of binary events. Our goal is twofold. First, we want the learning algorithm to be no-regret with respect to the best fixed expert in hindsight. Second, we want incentive compatibility, a guarantee that each expert's best strategy is to report his true beliefs about the realization of each event. To achieve this goal, we build on the literature on wagering mechanisms, a type of multi-agent scoring rule. We provide algorithms that achieve no regret and incentive compatibility for myopic experts for both the full and partial information settings. In experiments on datasets from FiveThirtyEight, our algorithms have regret comparable to classic no-regret algorithms, which are not incentive-compatible. Finally, we identify an incentive-compatible algorithm for forward-looking strategic agents that exhibits diminishing regret in practice.

Crowdsourced Outcome Determination in Prediction Markets

A prediction market is a useful means of aggregating information about a future event. To function, the market needs a trusted entity who will verify the true outcome in the end. Motivated by the recent introduction of decentralized prediction markets, we introduce a mechanism that allows for the outcome to be determined by the votes of a group of arbiters who may themselves hold stakes in the market. Despite the potential conflict of interest, we derive conditions under which we can incentivize arbiters to vote truthfully by using funds raised from market fees to implement a peer prediction mechanism. Finally, we investigate what parameter values could be used in a real-world implementation of our mechanism.

The Possibilities and Limitations of Private Prediction Markets

We consider the design of private prediction markets, financial markets designed to elicit predictions about uncertain events without revealing too much information about market participants' actions or beliefs. Our goal is to design market mechanisms in which participants' trades or wagers influence the market's behavior in a way that leads to accurate predictions, yet no single participant has too much influence over what others are able to observe. We study the possibilities and limitations of such mechanisms using tools from differential privacy. We begin by designing a private one-shot wagering mechanism in which bettors specify a belief about the likelihood of a future event and a corresponding monetary wager. Wagers are redistributed among bettors in a way that more highly rewards those with accurate predictions. We provide a class of wagering mechanisms that are guaranteed to satisfy truthfulness, budget balance in expectation, and other desirable properties while additionally guaranteeing epsilon-joint differential privacy in the bettors' reported beliefs, and analyze the trade-off between the achievable level of privacy and the sensitivity of a bettor's payment to her own report. We then ask whether it is possible to obtain privacy in dynamic prediction markets, focusing our attention on the popular cost-function framework in which securities with payments linked to future events are bought and sold by an automated market maker. We show that under general conditions, it is impossible for such a market maker to simultaneously achieve bounded worst-case loss and epsilon-differential privacy without allowing the privacy guarantee to degrade extremely quickly as the number of trades grows, making such markets impractical in settings in which privacy is valued. We conclude by suggesting several avenues for potentially circumventing this lower bound.

Budget Constraints in Prediction Markets

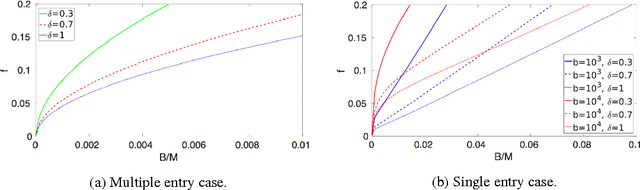
We give a detailed characterization of optimal trades under budget constraints in a prediction market with a cost-function-based automated market maker. We study how the budget constraints of individual traders affect their ability to impact the market price. As a concrete application of our characterization, we give sufficient conditions for a property we call budget additivity: two traders with budgets B and B' and the same beliefs would have a combined impact equal to a single trader with budget B+B'. That way, even if a single trader cannot move the market much, a crowd of like-minded traders can have the same desired effect. When the set of payoff vectors associated with outcomes, with coordinates corresponding to securities, is affinely independent, we obtain that a generalization of the heavily-used logarithmic market scoring rule is budget additive, but the quadratic market scoring rule is not. Our results may be used both descriptively, to understand if a particular market maker is affected by budget constraints or not, and prescriptively, as a recipe to construct markets.

Toward a Market Model for Bayesian Inference

We present a methodology for representing probabilistic relationships in a general-equilibrium economic model. Specifically, we define a precise mapping from a Bayesian network with binary nodes to a market price system where consumers and producers trade in uncertain propositions. We demonstrate the correspondence between the equilibrium prices of goods in this economy and the probabilities represented by the Bayesian network. A computational market model such as this may provide a useful framework for investigations of belief aggregation, distributed probabilistic inference, resource allocation under uncertainty, and other problems of decentralized uncertainty.

Representing Aggregate Belief through the Competitive Equilibrium of a Securities Market

We consider the problem of belief aggregation: given a group of individual agents with probabilistic beliefs over a set of uncertain events, formulate a sensible consensus or aggregate probability distribution over these events. Researchers have proposed many aggregation methods, although on the question of which is best the general consensus is that there is no consensus. We develop a market-based approach to this problem, where agents bet on uncertain events by buying or selling securities contingent on their outcomes. Each agent acts in the market so as to maximize expected utility at given securities prices, limited in its activity only by its own risk aversion. The equilibrium prices of goods in this market represent aggregate beliefs. For agents with constant risk aversion, we demonstrate that the aggregate probability exhibits several desirable properties, and is related to independently motivated techniques. We argue that the market-based approach provides a plausible mechanism for belief aggregation in multiagent systems, as it directly addresses self-motivated agent incentives for participation and for truthfulness, and can provide a decision-theoretic foundation for the "expert weights" often employed in centralized pooling techniques.

Logarithmic Time Parallel Bayesian Inference

I present a parallel algorithm for exact probabilistic inference in Bayesian networks. For polytree networks with n variables, the worst-case time complexity is O(log n) on a CREW PRAM (concurrent-read, exclusive-write parallel random-access machine) with n processors, for any constant number of evidence variables. For arbitrary networks, the time complexity is O(r^{3w}*log n) for n processors, or O(w*log n) for r^{3w}*n processors, where r is the maximum range of any variable, and w is the induced width (the maximum clique size), after moralizing and triangulating the network.

Graphical Representations of Consensus Belief

Graphical models based on conditional independence support concise encodings of the subjective belief of a single agent. A natural question is whether the consensus belief of a group of agents can be represented with equal parsimony. We prove, under relatively mild assumptions, that even if everyone agrees on a common graph topology, no method of combining beliefs can maintain that structure. Even weaker conditions rule out local aggregation within conditional probability tables. On a more positive note, we show that if probabilities are combined with the logarithmic opinion pool (LogOP), then commonly held Markov independencies are maintained. This suggests a straightforward procedure for constructing a consensus Markov network. We describe an algorithm for computing the LogOP with time complexity comparable to that of exact Bayesian inference.

Price Updating in Combinatorial Prediction Markets with Bayesian Networks

To overcome the #P-hardness of computing/updating prices in logarithm market scoring rule-based (LMSR-based) combinatorial prediction markets, Chen et al. [5] recently used a simple Bayesian network to represent the prices of securities in combinatorial predictionmarkets for tournaments, and showed that two types of popular securities are structure preserving. In this paper, we significantly extend this idea by employing Bayesian networks in general combinatorial prediction markets. We reveal a very natural connection between LMSR-based combinatorial prediction markets and probabilistic belief aggregation,which leads to a complete characterization of all structure preserving securities for decomposable network structures. Notably, the main results by Chen et al. [5] are corollaries of our characterization. We then prove that in order for a very basic set of securities to be structure preserving, the graph of the Bayesian network must be decomposable. We also discuss some approximation techniques for securities that are not structure preserving.