Proportionally Representative Clustering

In recent years, there has been a surge in effort to formalize notions of fairness in machine learning. We focus on clustering -- one of the fundamental tasks in unsupervised machine learning. We propose a new axiom that captures proportional representation fairness (PRF). We make a case that the concept achieves the raison d'{\^{e}}tre of several existing concepts in the literature in an arguably more convincing manner. Our fairness concept is not satisfied by existing fair clustering algorithms. We design efficient algorithms to achieve PRF both for unconstrained and discrete clustering problems.

Strategyproof and Proportionally Fair Facility Location

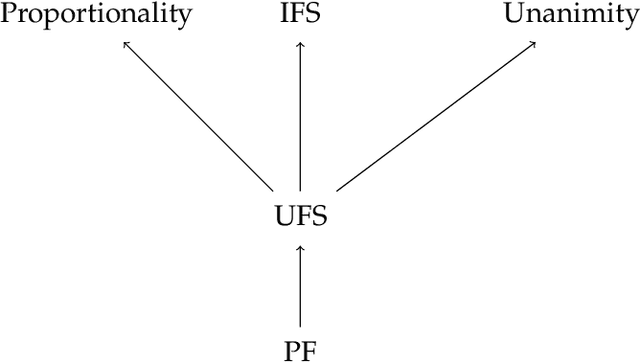
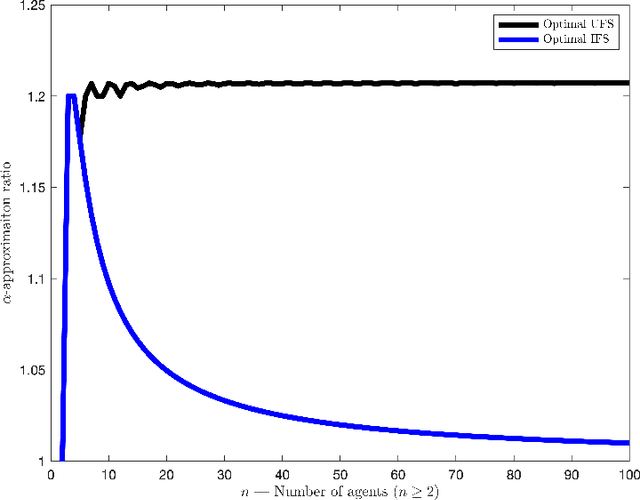
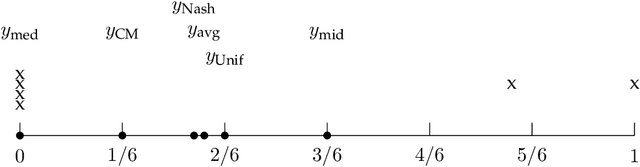
We focus on a simple, one-dimensional collective decision problem (often referred to as the facility location problem) and explore issues of strategyproofness and proportional fairness. We present several characterization results for mechanisms that satisfy strategyproofness and varying levels of proportional fairness. We also characterize one of the mechanisms as the unique equilibrium outcome for any mechanism that satisfies natural fairness and monotonicity properties. Finally, we identify strategyproof and proportionally fair mechanisms that provide the best welfare-optimal approximation among all mechanisms that satisfy the corresponding fairness axiom.

A characterization of proportionally representative committees

A well-known axiom for proportional representation is Proportionality of Solid Coalitions (PSC). We characterize committees satisfying PSC as possible outcomes of the Minimal Demand rule, which generalizes an approach pioneered by Michael Dummett.

Facility Location Problem with Capacity Constraints: Algorithmic and Mechanism Design Perspectives

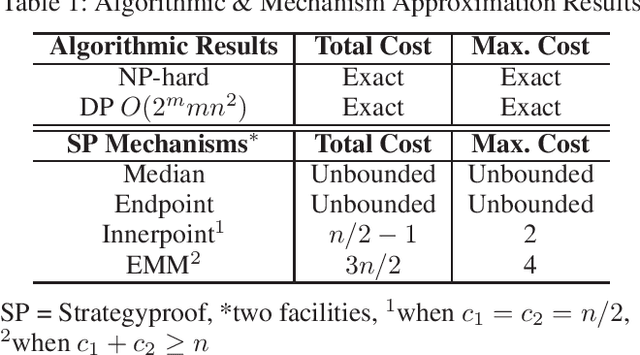
We consider the facility location problem in the one-dimensional setting where each facility can serve a limited number of agents from the algorithmic and mechanism design perspectives. From the algorithmic perspective, we prove that the corresponding optimization problem, where the goal is to locate facilities to minimize either the total cost to all agents or the maximum cost of any agent is NP-hard. However, we show that the problem is fixed-parameter tractable, and the optimal solution can be computed in polynomial time whenever the number of facilities is bounded, or when all facilities have identical capacities. We then consider the problem from a mechanism design perspective where the agents are strategic and need not reveal their true locations. We show that several natural mechanisms studied in the uncapacitated setting either lose strategyproofness or a bound on the solution quality for the total or maximum cost objective. We then propose new mechanisms that are strategyproof and achieve approximation guarantees that almost match the lower bounds.

Mechanism Design without Money for Common Goods

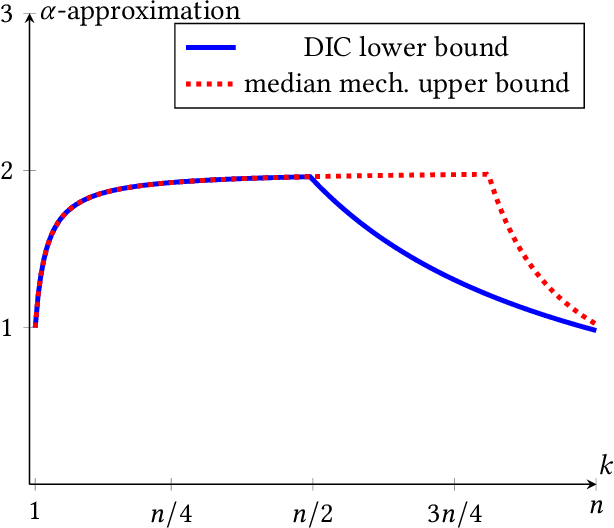
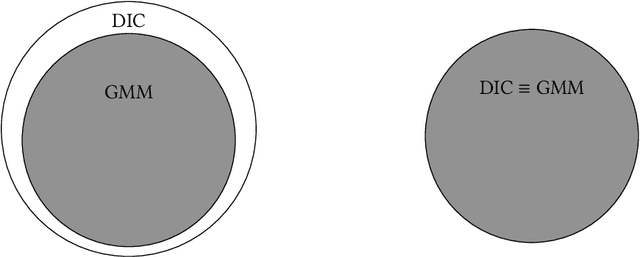
We initiate the study of mechanism design without money for common goods. Our model captures a variation of the well-known one-dimensional facility location problem if the facility is assumed to have a capacity constraint $k<n$ where $n$ is the population size. This new model introduces a richer game-theoretic context compared to the classical facility location, or public goods, problem. Our key result contributes a novel perspective relating to the "major open question" (Barbar\`a et al., 1998) posed by Border and Jordan (1983) by showing the equivalence of dominant strategy incentive compatible (DIC) mechanisms for common goods and the family of Generalized Median Mechanisms (GMMs). This equivalence does not hold in the public goods setting and, by situating GMMs in this broader game-theoretic context, is the first complete characterization of GMMs in terms of purely strategic properties. We then characterize lower bounds of the welfare approximation ratio across all DIC mechanisms and identify a DIC mechanism which attains this lower bound when $k<\lceil (n+1)/2\rceil$ and $k=n$. Finally, we analyze the approximation ratio when the property of DIC is weakened to ex post incentive compatibility.

Representing the Insincere: Strategically Robust Proportional Representation

Proportional representation (PR) is a fundamental principle of many democracies world-wide which employ PR-based voting rules to elect their representatives. The normative properties of these voting rules however, are often only understood in the context of sincere voting. In this paper we consider PR in the presence of strategic voters. We construct a voting rule such that for every preference profile there exists at least one costly voting equilibrium satisfying PR with respect to voters' private and unrevealed preferences - such a voting rule is said to be strategically robust. In contrast, a commonly applied voting rule is shown not be strategically robust. Furthermore, we prove a limit on `how strategically robust' a PR-based voting rule can be; we show that there is no PR-based voting rule which ensures that every equilibrium satisfies PR. Collectively, our results highlight the possibility and limit of achieving PR in the presence of strategic voters and a positive role for mechanisms, such as pre-election polls, which coordinate voter behaviour towards equilibria which satisfy PR.

Sub-committee Approval Voting and Generalised Justified Representation Axioms

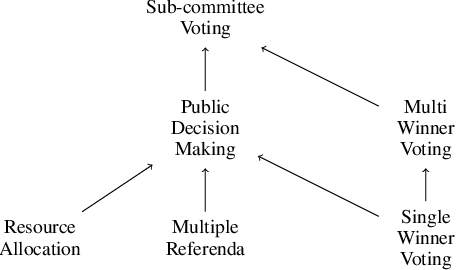
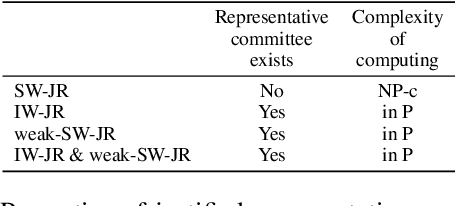
Social choice is replete with various settings including single-winner voting, multi-winner voting, probabilistic voting, multiple referenda, and public decision making. We study a general model of social choice called Sub-Committee Voting (SCV) that simultaneously generalizes these settings. We then focus on sub-committee voting with approvals and propose extensions of the justified representation axioms that have been considered for proportional representation in approval-based committee voting. We study the properties and relations of these axioms. For each of the axioms, we analyse whether a representative committee exists and also examine the complexity of computing and verifying such a committee.