Facility Location Games with Scaling Effects

We take the classic facility location problem and consider a variation, in which each agent's individual cost function is equal to their distance from the facility multiplied by a scaling factor which is determined by the facility placement. In addition to the general class of continuous scaling functions, we also provide results for piecewise linear scaling functions which can effectively approximate or model the scaling of many real world scenarios. We focus on the objectives of total and maximum cost, describing the computation of the optimal solution. We then move to the approximate mechanism design setting, observing that the agents' preferences may no longer be single-peaked. Consequently, we characterize the conditions on scaling functions which ensure that agents have single-peaked preferences. Under these conditions, we find results on the total and maximum cost approximation ratios achievable by strategyproof and anonymous mechanisms.

Mixed Strategies for Security Games with General Defending Requirements

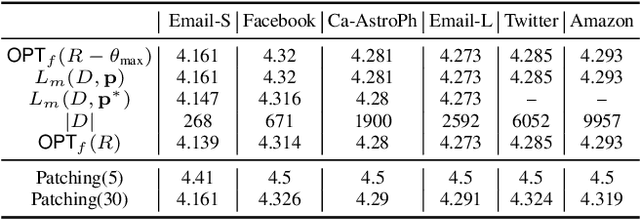
The Stackelberg security game is played between a defender and an attacker, where the defender needs to allocate a limited amount of resources to multiple targets in order to minimize the loss due to adversarial attack by the attacker. While allowing targets to have different values, classic settings often assume uniform requirements to defend the targets. This enables existing results that study mixed strategies (randomized allocation algorithms) to adopt a compact representation of the mixed strategies. In this work, we initiate the study of mixed strategies for the security games in which the targets can have different defending requirements. In contrast to the case of uniform defending requirement, for which an optimal mixed strategy can be computed efficiently, we show that computing the optimal mixed strategy is NP-hard for the general defending requirements setting. However, we show that strong upper and lower bounds for the optimal mixed strategy defending result can be derived. We propose an efficient close-to-optimal Patching algorithm that computes mixed strategies that use only few pure strategies. We also study the setting when the game is played on a network and resource sharing is enabled between neighboring targets. Our experimental results demonstrate the effectiveness of our algorithm in several large real-world datasets.

Maximizing approximately k-submodular functions

We introduce the problem of maximizing approximately $k$-submodular functions subject to size constraints. In this problem, one seeks to select $k$-disjoint subsets of a ground set with bounded total size or individual sizes, and maximum utility, given by a function that is "close" to being $k$-submodular. The problem finds applications in tasks such as sensor placement, where one wishes to install $k$ types of sensors whose measurements are noisy, and influence maximization, where one seeks to advertise $k$ topics to users of a social network whose level of influence is uncertain. To deal with the problem, we first provide two natural definitions for approximately $k$-submodular functions and establish a hierarchical relationship between them. Next, we show that simple greedy algorithms offer approximation guarantees for different types of size constraints. Last, we demonstrate experimentally that the greedy algorithms are effective in sensor placement and influence maximization problems.

Defending with Shared Resources on a Network

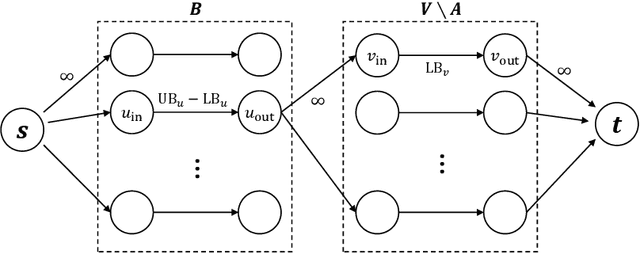
In this paper we consider a defending problem on a network. In the model, the defender holds a total defending resource of R, which can be distributed to the nodes of the network. The defending resource allocated to a node can be shared by its neighbors. There is a weight associated with every edge that represents the efficiency defending resources are shared between neighboring nodes. We consider the setting when each attack can affect not only the target node, but its neighbors as well. Assuming that nodes in the network have different treasures to defend and different defending requirements, the defender aims at allocating the defending resource to the nodes to minimize the loss due to attack. We give polynomial time exact algorithms for two important special cases of the network defending problem. For the case when an attack can only affect the target node, we present an LP-based exact algorithm. For the case when defending resources cannot be shared, we present a max-flow-based exact algorithm. We show that the general problem is NP-hard, and we give a 2-approximation algorithm based on LP-rounding. Moreover, by giving a matching lower bound of 2 on the integrality gap on the LP relaxation, we show that our rounding is tight.