Mixed Strategies for Security Games with General Defending Requirements

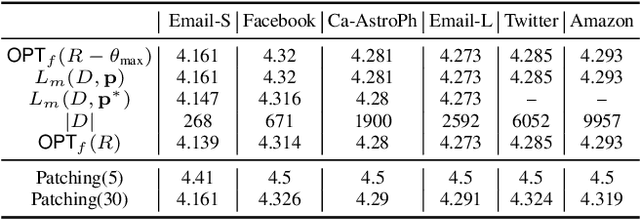
The Stackelberg security game is played between a defender and an attacker, where the defender needs to allocate a limited amount of resources to multiple targets in order to minimize the loss due to adversarial attack by the attacker. While allowing targets to have different values, classic settings often assume uniform requirements to defend the targets. This enables existing results that study mixed strategies (randomized allocation algorithms) to adopt a compact representation of the mixed strategies. In this work, we initiate the study of mixed strategies for the security games in which the targets can have different defending requirements. In contrast to the case of uniform defending requirement, for which an optimal mixed strategy can be computed efficiently, we show that computing the optimal mixed strategy is NP-hard for the general defending requirements setting. However, we show that strong upper and lower bounds for the optimal mixed strategy defending result can be derived. We propose an efficient close-to-optimal Patching algorithm that computes mixed strategies that use only few pure strategies. We also study the setting when the game is played on a network and resource sharing is enabled between neighboring targets. Our experimental results demonstrate the effectiveness of our algorithm in several large real-world datasets.

Generalized Spatially-Coupled Parallel Concatenated Codes With Partial Repetition

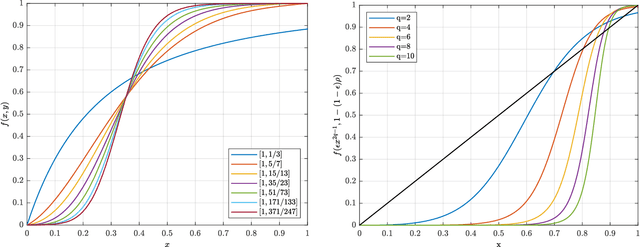
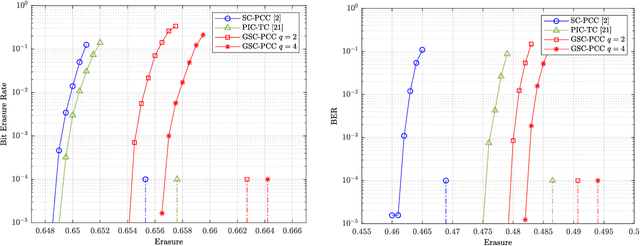
A new class of spatially-coupled turbo-like codes (SC-TCs), dubbed generalized spatially coupled parallel concatenated codes (GSC-PCCs), is introduced. These codes are constructed by applying spatial coupling on parallel concatenated codes (PCCs) with a fraction of information bits repeated $q$ times. GSC-PCCs can be seen as a generalization of the original spatially-coupled parallel concatenated codes proposed by Moloudi et al. [2]. To characterize the asymptotic performance of GSC-PCCs, we derive the corresponding density evolution equations and compute their decoding thresholds. The threshold saturation effect is observed and proven. Most importantly, we rigorously prove that any rate-$R$ GSC-PCC ensemble with 2-state convolutional component codes achieves at least a fraction $1-\frac{R}{R+q}$ of the capacity of the binary erasure channel (BEC) for repetition factor $q\geq2$ and this multiplicative gap vanishes as $q$ tends to infinity. To the best of our knowledge, this is the first class of SC-TCs that are proven to be capacity-achieving. Further, the connection between the strength of the component codes, the decoding thresholds of GSC-PCCs, and the repetition factor are established. The superiority of the proposed codes with finite blocklength is exemplified by comparing their error performance with that of existing SC-TCs via computer simulations.

Generalized Spatially Coupled Parallel Concatenated Convolutional Codes With Partial Repetition

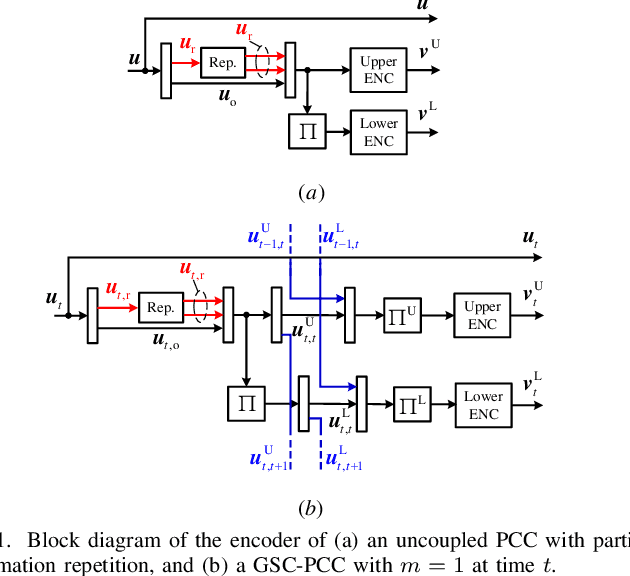
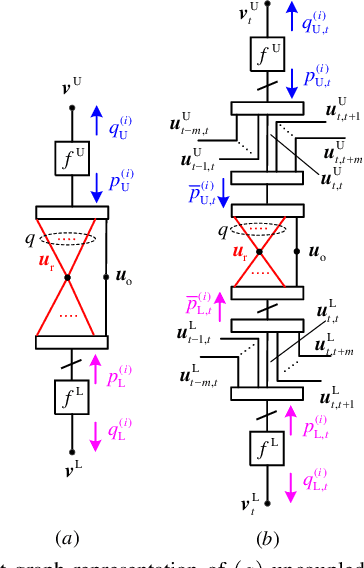
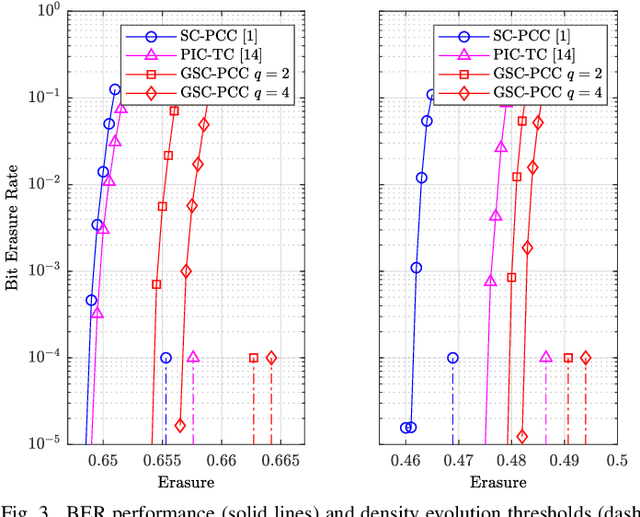
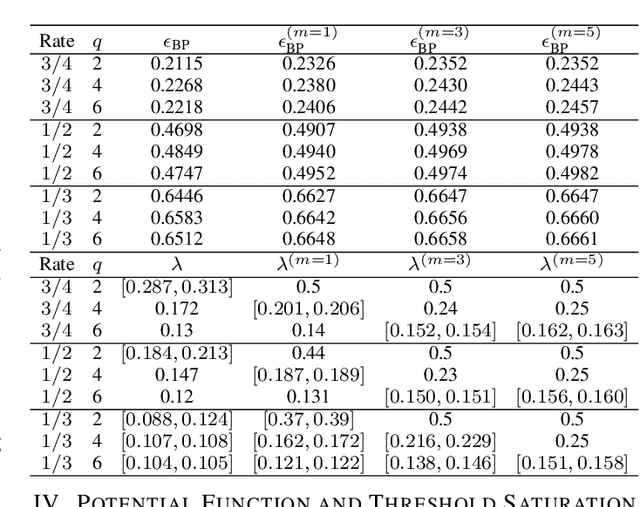
We introduce generalized spatially coupled parallel concatenated codes (GSC-PCCs), a class of spatially coupled turbo-like codes obtained by coupling parallel concatenated codes (PCCs) with a fraction of information bits repeated before the PCC encoding. GSC-PCCs can be seen as a generalization of the original spatially coupled parallel concatenated convolutional codes (SC-PCCs) proposed by Moloudi et al. [1]. To characterize the asymptotic performance of GSC-PCCs, we derive the corresponding density evolution equations and compute their decoding thresholds. We show that the proposed codes have some nice properties such as threshold saturation and that their decoding thresholds improve with the repetition factor $q$. Most notably, our analysis suggests that the proposed codes asymptotically approach the capacity as $q$ tends to infinity with any given constituent convolutional code.

Analysis and Design of Partially Information- and Partially Parity-Coupled Turbo Codes

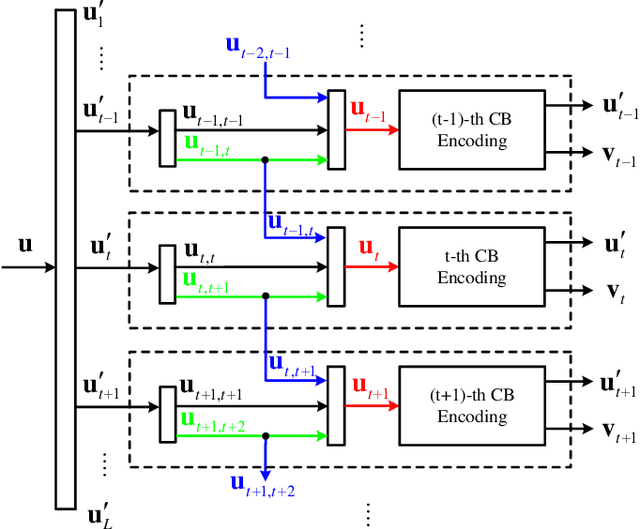
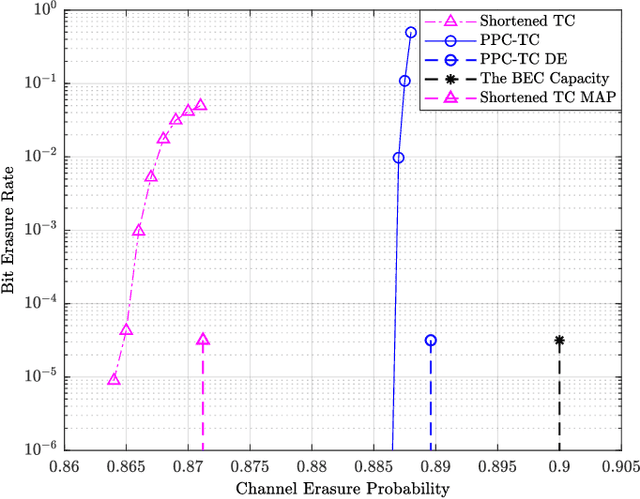
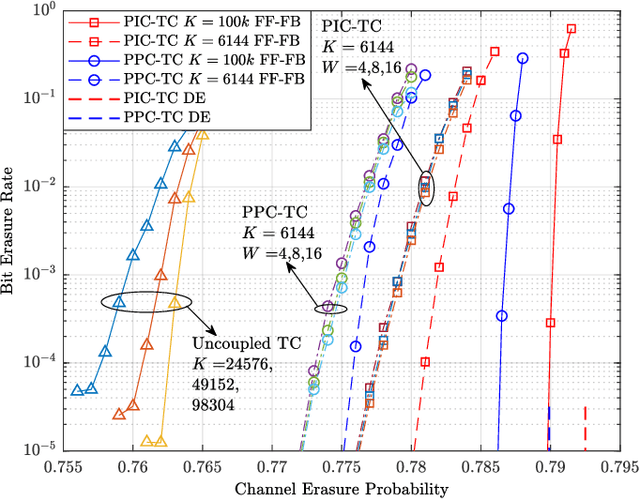
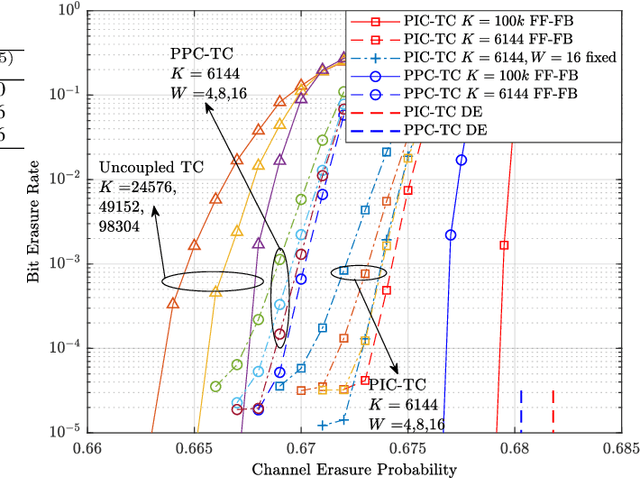
In this paper, we study a class of spatially coupled turbo codes, namely partially information- and partially parity-coupled turbo codes. This class of codes enjoy several advantages such as flexible code rate adjustment by varying the coupling ratio and the encoding and decoding architectures of the underlying component codes can remain unchanged. For this work, we first provide the construction methods for partially coupled turbo codes with coupling memory $m$ and study the corresponding graph models. We then derive the density evolution equations for the corresponding ensembles on the binary erasure channel to precisely compute their iterative decoding thresholds. Rate-compatible designs and their decoding thresholds are also provided, where the coupling and puncturing ratios are jointly optimized to achieve the largest decoding threshold for a given target code rate. Our results show that for a wide range of code rates, the proposed codes attain close-to-capacity performance and the decoding performance improves with increasing the coupling memory. In particular, the proposed partially parity-coupled turbo codes have thresholds within 0.0002 of the BEC capacity for rates ranging from $1/3$ to $9/10$, yielding an attractive way for constructing rate-compatible capacity-approaching channel codes.

Recreating Bat Behavior on Quad-rotor UAVs-A Simulation Approach

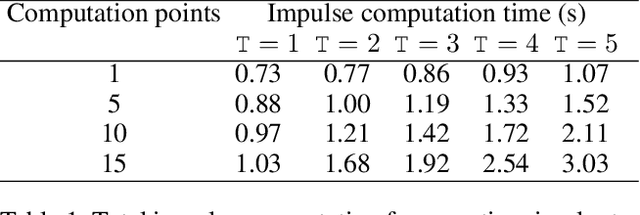
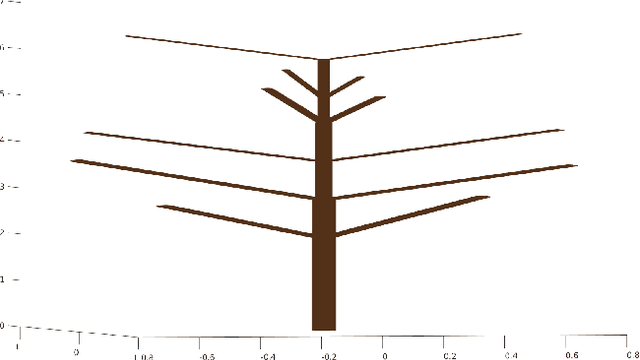
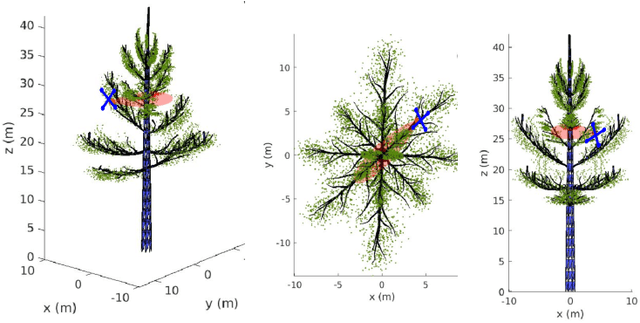
We develop an effective computer model to simulate sensing environments that consist of natural trees. The simulated environments are random and contain full geometry of the tree foliage. While this simulated model can be used as a general platform for studying the sensing mechanism of different flying species, our ultimate goal is to build bat-inspired Quad-rotor UAVs- UAVs that can recreate bat's flying behavior (e.g., obstacle avoidance, path planning) in dense vegetation. To this end, we also introduce an foliage echo simulator that can produce simulated echoes by mimicking bat's biosonar. In our current model, a few realistic model choices or assumptions are made. First, in order to create natural looking trees, the branching structures of trees are modeled by L-systems, whereas the detailed geometry of branches, sub-branches and leaves is created by randomizing a reference tree in a CAD object file. Additionally, the foliage echo simulator is simplified so that no shading effect is considered. We demonstrate our developed model by simulating real-world scenarios with multiple trees and compute the corresponding impulse responses along a Quad-rotor trajectory.

Simulate forest trees by integrating L-system and 3D CAD files

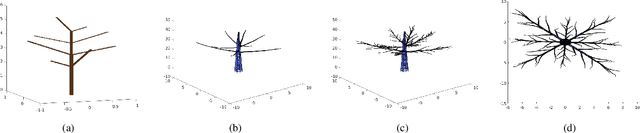
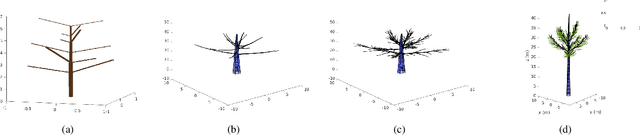
In this article, we propose a new approach for simulating trees, including their branches, sub-branches, and leaves. This approach combines the theory of biological development, mathematical models, and computer graphics, producing simulated trees and forest with full geometry. Specifically, we adopt the Lindenmayer process to simulate the branching pattern of trees and modify the available measurements and dimensions of 3D CAD developed object files to create natural looking sub-branches and leaves. Randomization has been added to the placement of all branches, sub branches and leaves. To simulate a forest, we adopt Inhomogeneous Poisson process to generate random locations of trees. Our approach can be used to create complex structured 3D virtual environment for the purpose of testing new sensors and training robotic algorithms. We look forward to applying this approach to test biosonar sensors that mimick bats' fly in the simulated environment.

Defending with Shared Resources on a Network

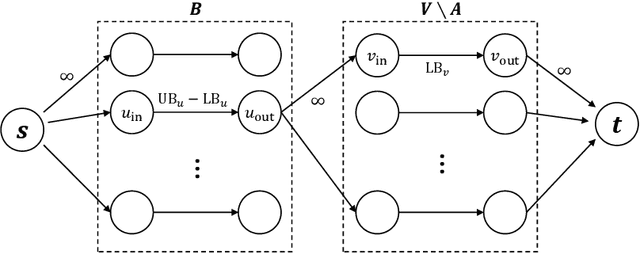
In this paper we consider a defending problem on a network. In the model, the defender holds a total defending resource of R, which can be distributed to the nodes of the network. The defending resource allocated to a node can be shared by its neighbors. There is a weight associated with every edge that represents the efficiency defending resources are shared between neighboring nodes. We consider the setting when each attack can affect not only the target node, but its neighbors as well. Assuming that nodes in the network have different treasures to defend and different defending requirements, the defender aims at allocating the defending resource to the nodes to minimize the loss due to attack. We give polynomial time exact algorithms for two important special cases of the network defending problem. For the case when an attack can only affect the target node, we present an LP-based exact algorithm. For the case when defending resources cannot be shared, we present a max-flow-based exact algorithm. We show that the general problem is NP-hard, and we give a 2-approximation algorithm based on LP-rounding. Moreover, by giving a matching lower bound of 2 on the integrality gap on the LP relaxation, we show that our rounding is tight.