Generalized Spatially-Coupled Parallel Concatenated Codes With Partial Repetition
Paper and Code
Jan 24, 2022

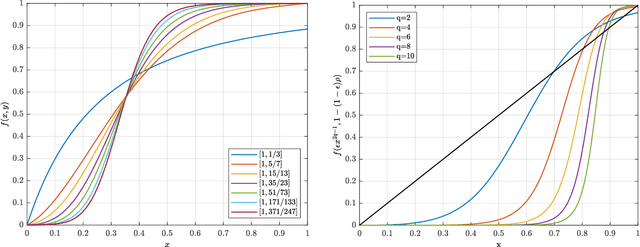
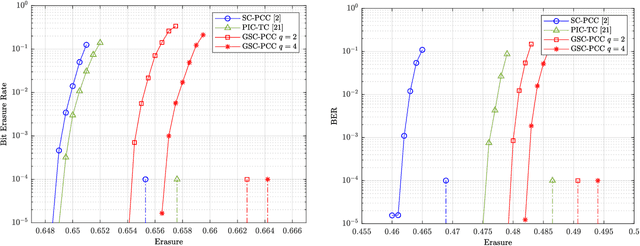
A new class of spatially-coupled turbo-like codes (SC-TCs), dubbed generalized spatially coupled parallel concatenated codes (GSC-PCCs), is introduced. These codes are constructed by applying spatial coupling on parallel concatenated codes (PCCs) with a fraction of information bits repeated $q$ times. GSC-PCCs can be seen as a generalization of the original spatially-coupled parallel concatenated codes proposed by Moloudi et al. [2]. To characterize the asymptotic performance of GSC-PCCs, we derive the corresponding density evolution equations and compute their decoding thresholds. The threshold saturation effect is observed and proven. Most importantly, we rigorously prove that any rate-$R$ GSC-PCC ensemble with 2-state convolutional component codes achieves at least a fraction $1-\frac{R}{R+q}$ of the capacity of the binary erasure channel (BEC) for repetition factor $q\geq2$ and this multiplicative gap vanishes as $q$ tends to infinity. To the best of our knowledge, this is the first class of SC-TCs that are proven to be capacity-achieving. Further, the connection between the strength of the component codes, the decoding thresholds of GSC-PCCs, and the repetition factor are established. The superiority of the proposed codes with finite blocklength is exemplified by comparing their error performance with that of existing SC-TCs via computer simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge