SPOT: Spatio-Temporal Obstacle-free Trajectory Planning for UAVs in an Unknown Dynamic Environment

We address the problem of reactive motion planning for quadrotors operating in unknown environments with dynamic obstacles. Our approach leverages a 4-dimensional spatio-temporal planner, integrated with vision-based Safe Flight Corridor (SFC) generation and trajectory optimization. Unlike prior methods that rely on map fusion, our framework is mapless, enabling collision avoidance directly from perception while reducing computational overhead. Dynamic obstacles are detected and tracked using a vision-based object segmentation and tracking pipeline, allowing robust classification of static versus dynamic elements in the scene. To further enhance robustness, we introduce a backup planning module that reactively avoids dynamic obstacles when no direct path to the goal is available, mitigating the risk of collisions during deadlock situations. We validate our method extensively in both simulation and real-world hardware experiments, and benchmark it against state-of-the-art approaches, showing significant advantages for reactive UAV navigation in dynamic, unknown environments.

The Llama 4 Herd: Architecture, Training, Evaluation, and Deployment Notes

This document consolidates publicly reported technical details about Metas Llama 4 model family. It summarizes (i) released variants (Scout and Maverick) and the broader herd context including the previewed Behemoth teacher model, (ii) architectural characteristics beyond a high-level MoE description covering routed/shared-expert structure, early-fusion multimodality, and long-context design elements reported for Scout (iRoPE and length generalization strategies), (iii) training disclosures spanning pre-training, mid-training for long-context extension, and post-training methodology (lightweight SFT, online RL, and lightweight DPO) as described in release materials, (iv) developer-reported benchmark results for both base and instruction-tuned checkpoints, and (v) practical deployment constraints observed across major serving environments, including provider-specific context limits and quantization packaging. The manuscript also summarizes licensing obligations relevant to redistribution and derivative naming, and reviews publicly described safeguards and evaluation practices. The goal is to provide a compact technical reference for researchers and practitioners who need precise, source-backed facts about Llama 4.

Locally Optimal Solutions to Constraint Displacement Problems via Path-Obstacle Overlaps

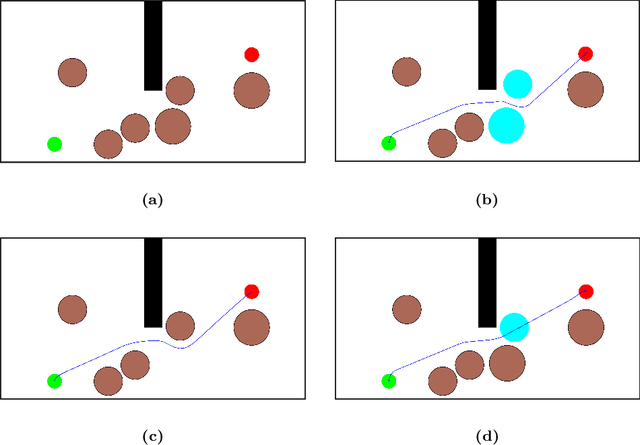
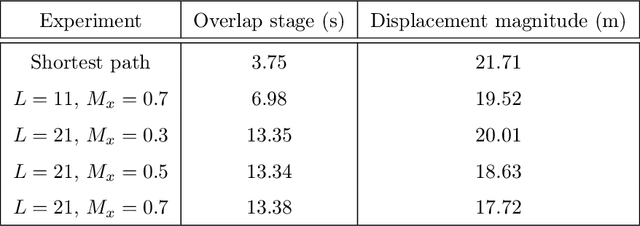
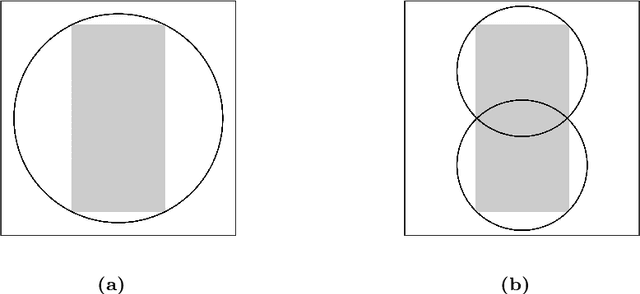
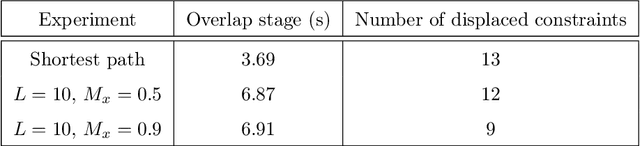
We present a unified approach for constraint displacement problems in which a robot finds a feasible path by displacing constraints or obstacles. To this end, we propose a two stage process that returns locally optimal obstacle displacements to enable a feasible path for the robot. The first stage proceeds by computing a trajectory through the obstacles while minimizing an appropriate objective function. In the second stage, these obstacles are displaced to make the computed robot trajectory feasible, that is, collision-free. Several examples are provided that successfully demonstrate our approach on two distinct classes of constraint displacement problems.

A Task and Motion Planning Framework Using Iteratively Deepened AND/OR Graph Networks

In this paper, we present an approach for integrated task and motion planning based on an AND/OR graph network, which is used to represent task-level states and actions, and we leverage it to implement different classes of task and motion planning problems (TAMP). Several problems that fall under task and motion planning do not have a predetermined number of sub-tasks to achieve a goal. For example, while retrieving a target object from a cluttered workspace, in principle the number of object re-arrangements required to finally grasp it cannot be known ahead of time. To address this challenge, and in contrast to traditional planners, also those based on AND/OR graphs, we grow the AND/OR graph at run-time by progressively adding sub-graphs until grasping the target object becomes feasible, which yields a network of AND/OR graphs. The approach is extended to enable multi-robot task and motion planning, and (i) it allows us to perform task allocation while coordinating the activity of a given number of robots, and (ii) can handle multi-robot tasks involving an a priori unknown number of sub-tasks. The approach is evaluated and validated both in simulation and with a real dual-arm robot manipulator, that is, Baxter from Rethink Robotics. In particular, for the single-robot task and motion planning, we validated our approach in three different TAMP domains. Furthermore, we also use three different robots for simulation, namely, Baxter, Franka Emika Panda manipulators, and a PR2 robot. Experiments show that our approach can be readily scaled to scenarios with many objects and robots, and is capable of handling different classes of TAMP problems.

An Incremental Sampling and Segmentation-Based Approach for Motion Planning Infeasibility

We present a simple and easy-to-implement algorithm to detect plan infeasibility in kinematic motion planning. Our method involves approximating the robot's configuration space to a discrete space, where each degree of freedom has a finite set of values. The obstacle region separates the free configuration space into different connected regions. For a path to exist between the start and goal configurations, they must lie in the same connected region of the free space. Thus, to ascertain plan infeasibility, we merely need to sample adequate points from the obstacle region that isolate start and goal. Accordingly, we progressively construct the configuration space by sampling from the discretized space and updating the bitmap cells representing obstacle regions. Subsequently, we partition this partially built configuration space to identify different connected components within it and assess the connectivity of the start and goal cells. We illustrate this methodology on five different scenarios with configuration spaces having up to 5 degree-of-freedom (DOF).

Safe motion planning with environment uncertainty

We present an approach for safe motion planning under robot state and environment (obstacle and landmark location) uncertainties. To this end, we first develop an approach that accounts for the landmark uncertainties during robot localization. Existing planning approaches assume that the landmark locations are well known or are known with little uncertainty. However, this might not be true in practice. Noisy sensors and imperfect motions compound to the errors originating from the estimate of environment features. Moreover, possible occlusions and dynamic objects in the environment render imperfect landmark estimation. Consequently, not considering this uncertainty can wrongly localize the robot, leading to inefficient plans. Our approach thus incorporates the landmark uncertainty within the Bayes filter estimation framework. We also analyze the effect of considering this uncertainty and delineate the conditions under which it can be ignored. Second, we extend the state-of-the-art by computing an exact expression for the collision probability under Gaussian distributed robot motion, perception and obstacle location uncertainties. We formulate the collision probability process as a quadratic form in random variables. Under Gaussian distribution assumptions, an exact expression for collision probability is thus obtained which is computable in real-time. In contrast, existing approaches approximate the collision probability using upper-bounds that can lead to overly conservative estimate and thereby suboptimal plans. We demonstrate and evaluate our approach using a theoretical example and simulations. We also present a comparison of our approach to different state-of-the-art methods.

Revisiting the Minimum Constraint Removal Problem in Mobile Robotics

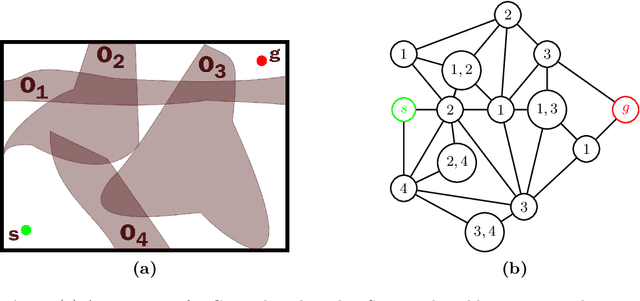
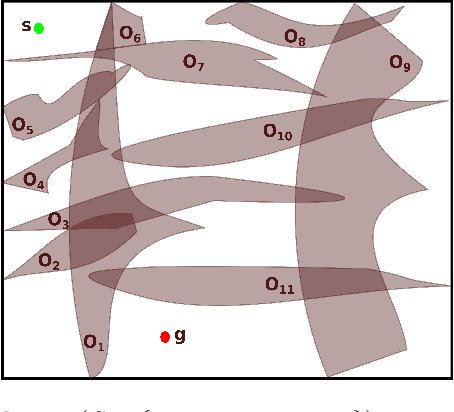
The minimum constraint removal problem seeks to find the minimum number of constraints, i.e., obstacles, that need to be removed to connect a start to a goal location with a collision-free path. This problem is NP-hard and has been studied in robotics, wireless sensing, and computational geometry. This work contributes to the existing literature by presenting and discussing two results. The first result shows that the minimum constraint removal is NP-hard for simply connected obstacles where each obstacle intersects a constant number of other obstacles. The second result demonstrates that for $n$ simply connected obstacles in the plane, instances of the minimum constraint removal problem with minimum removable obstacles lower than $(n+1)/3$ can be solved in polynomial time. This result is also empirically validated using several instances of randomly sampled axis-parallel rectangles.

Computational Tradeoff in Minimum Obstacle Displacement Planning for Robot Navigation

In this paper, we look into the minimum obstacle displacement (MOD) planning problem from a mobile robot motion planning perspective. This problem finds an optimal path to goal by displacing movable obstacles when no path exists due to collision with obstacles. However this problem is computationally expensive and grows exponentially in the size of number of movable obstacles. This work looks into approximate solutions that are computationally less intensive and differ from the optimal solution by a factor of the optimal cost.

Minimum Displacement Motion Planning for Movable Obstacles

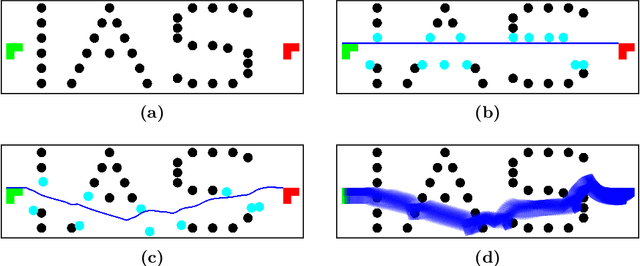
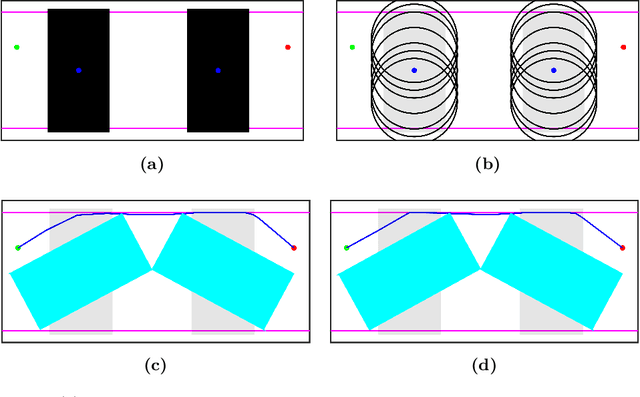
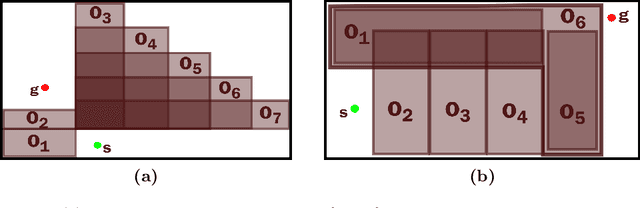
This paper presents a minimum displacement motion planning problem wherein obstacles are displaced by a minimum amount to find a feasible path. We define a metric for robot-obstacle intersection that measures the extent of the intersection and use this to penalize robot-obstacle overlaps. Employing the actual robot dynamics, the planner first finds a path through the obstacles that minimizes the robot-obstacle intersections. The metric is then used to iteratively displace the obstacles to achieve a feasible path. Several examples are provided that successfully demonstrates the proposed problem.

Exact and Bounded Collision Probability for Motion Planning under Gaussian Uncertainty

Computing collision-free trajectories is of prime importance for safe navigation. We present an approach for computing the collision probability under Gaussian distributed motion and sensing uncertainty with the robot and static obstacle shapes approximated as ellipsoids. The collision condition is formulated as the distance between ellipsoids and unlike previous approaches we provide a method for computing the exact collision probability. Furthermore, we provide a tight upper bound that can be computed much faster during online planning. Comparison to other state-of-the-art methods is also provided. The proposed method is evaluated in simulation under varying configuration and number of obstacles.