Minimax-Bayes Reinforcement Learning

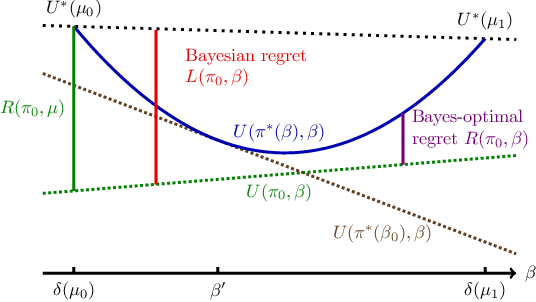
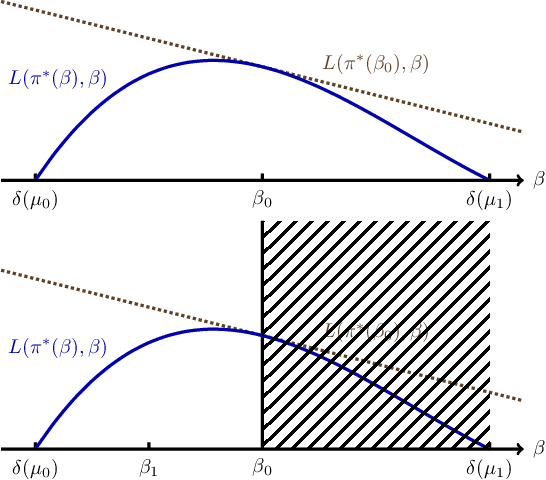
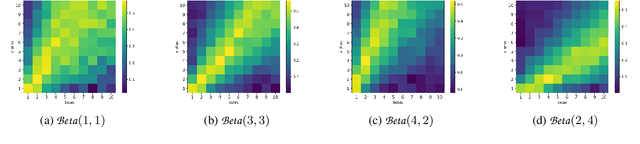
While the Bayesian decision-theoretic framework offers an elegant solution to the problem of decision making under uncertainty, one question is how to appropriately select the prior distribution. One idea is to employ a worst-case prior. However, this is not as easy to specify in sequential decision making as in simple statistical estimation problems. This paper studies (sometimes approximate) minimax-Bayes solutions for various reinforcement learning problems to gain insights into the properties of the corresponding priors and policies. We find that while the worst-case prior depends on the setting, the corresponding minimax policies are more robust than those that assume a standard (i.e. uniform) prior.

Adaptive Belief Discretization for POMDP Planning

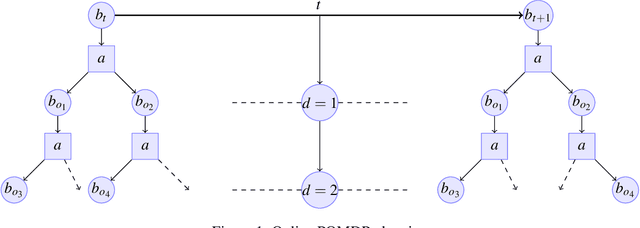
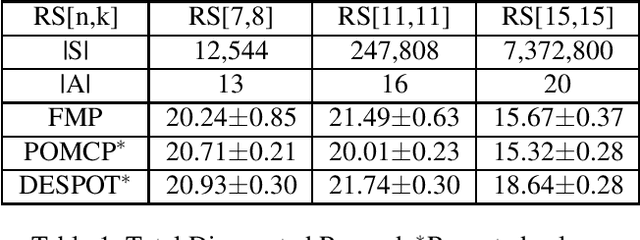
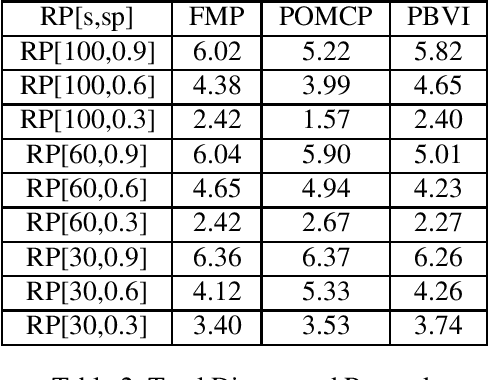
Partially Observable Markov Decision Processes (POMDP) is a widely used model to represent the interaction of an environment and an agent, under state uncertainty. Since the agent does not observe the environment state, its uncertainty is typically represented through a probabilistic belief. While the set of possible beliefs is infinite, making exact planning intractable, the belief space's complexity (and hence planning complexity) is characterized by its covering number. Many POMDP solvers uniformly discretize the belief space and give the planning error in terms of the (typically unknown) covering number. We instead propose an adaptive belief discretization scheme, and give its associated planning error. We furthermore characterize the covering number with respect to the POMDP parameters. This allows us to specify the exact memory requirements on the planner, needed to bound the value function error. We then propose a novel, computationally efficient solver using this scheme. We demonstrate that our algorithm is highly competitive with the state of the art in a variety of scenarios.

Inferential Induction: Joint Bayesian Estimation of MDPs and Value Functions

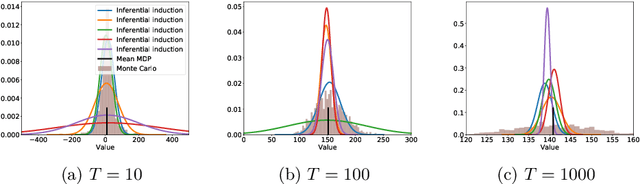
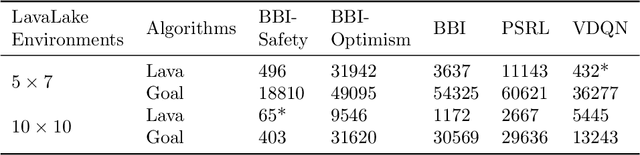
Bayesian reinforcement learning (BRL) offers a decision-theoretic solution to the problem of reinforcement learning. However, typical model-based BRL algorithms have focused either on ma intaining a posterior distribution on models or value functions and combining this with approx imate dynamic programming or tree search. This paper describes a novel backwards induction pri nciple for performing joint Bayesian estimation of models and value functions, from which many new BRL algorithms can be obtained. We demonstrate this idea with algorithms and experiments in discrete state spaces.

Deeper & Sparser Exploration

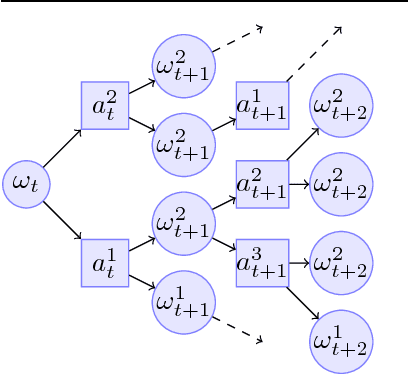
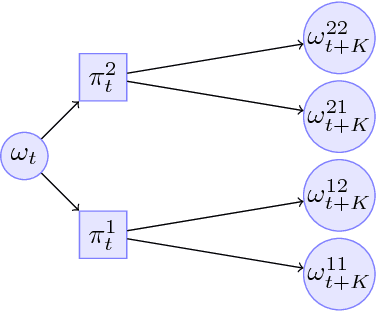
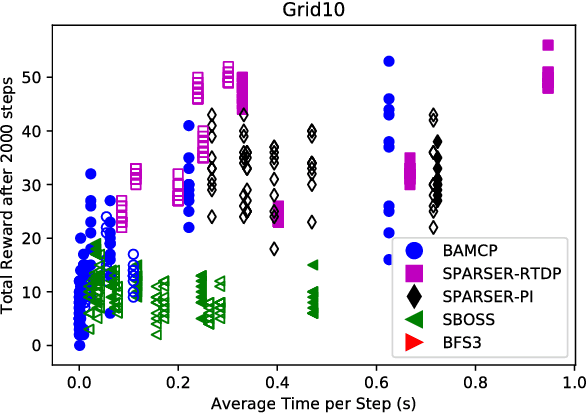
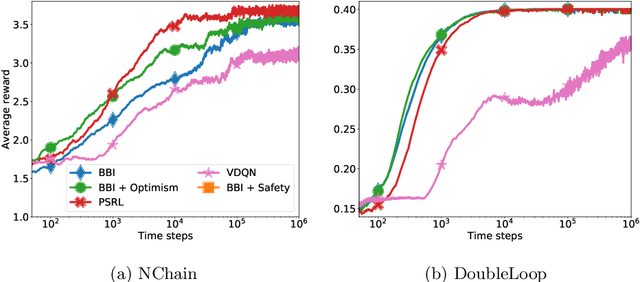
We address the problem of efficient exploration by proposing a new meta algorithm in the context of model-based online planning for Bayesian Reinforcement Learning (BRL). We beat the state-of-the-art, while staying computationally faster, in some cases by two orders of magnitude. This is the first Optimism free BRL algorithm to beat all previous state-of-the-art in tabular RL. The main novelty is the use of a candidate policy generator, to generate long-term options in the belief tree, which allows us to create much sparser and deeper trees. We present results on many standard environments and empirically prove its performance.