Adaptive Belief Discretization for POMDP Planning
Paper and Code
Apr 15, 2021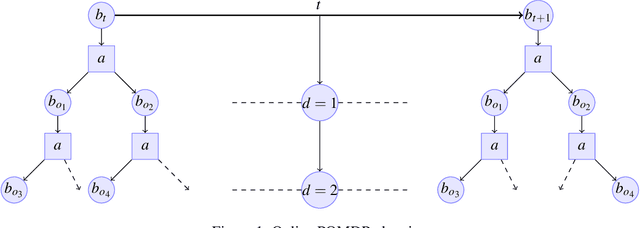
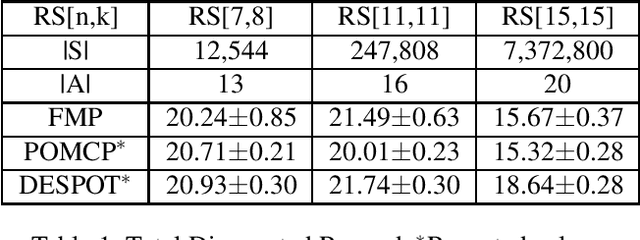
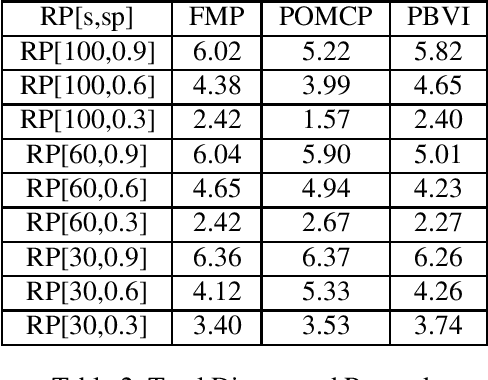
Partially Observable Markov Decision Processes (POMDP) is a widely used model to represent the interaction of an environment and an agent, under state uncertainty. Since the agent does not observe the environment state, its uncertainty is typically represented through a probabilistic belief. While the set of possible beliefs is infinite, making exact planning intractable, the belief space's complexity (and hence planning complexity) is characterized by its covering number. Many POMDP solvers uniformly discretize the belief space and give the planning error in terms of the (typically unknown) covering number. We instead propose an adaptive belief discretization scheme, and give its associated planning error. We furthermore characterize the covering number with respect to the POMDP parameters. This allows us to specify the exact memory requirements on the planner, needed to bound the value function error. We then propose a novel, computationally efficient solver using this scheme. We demonstrate that our algorithm is highly competitive with the state of the art in a variety of scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge