Fair Set Selection: Meritocracy and Social Welfare

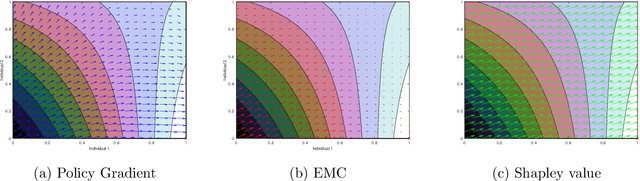
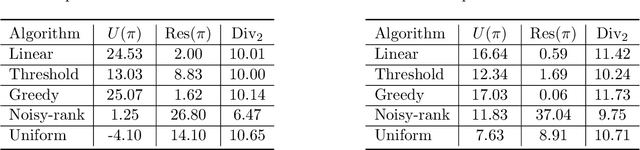
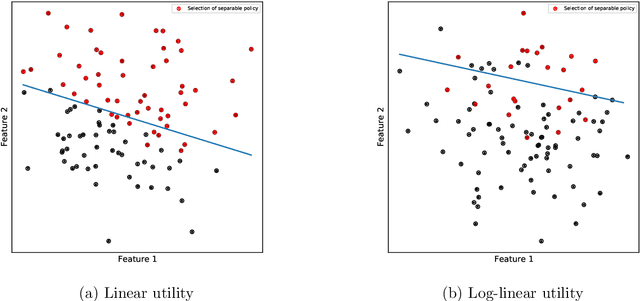
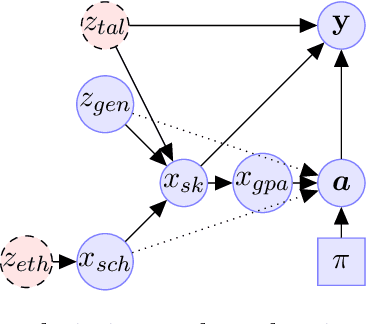
In this paper, we formulate the problem of selecting a set of individuals from a candidate population as a utility maximisation problem. From the decision maker's perspective, it is equivalent to finding a selection policy that maximises expected utility. Our framework leads to the notion of expected marginal contribution (EMC) of an individual with respect to a selection policy as a measure of deviation from meritocracy. In order to solve the maximisation problem, we propose to use a policy gradient algorithm. For certain policy structures, the policy gradients are proportional to EMCs of individuals. Consequently, the policy gradient algorithm leads to a locally optimal solution that has zero EMC, and satisfies meritocracy. For uniform policies, EMC reduces to the Shapley value. EMC also generalises the fair selection properties of Shapley value for general selection policies. We experimentally analyse the effect of different policy structures in a simulated college admission setting and compare with ranking and greedy algorithms. Our results verify that separable linear policies achieve high utility while minimising EMCs. We also show that we can design utility functions that successfully promote notions of group fairness, such as diversity.