Learning Probabilistic Temporal Logic Specifications for Stochastic Systems

There has been substantial progress in the inference of formal behavioural specifications from sample trajectories, for example, using Linear Temporal Logic (LTL). However, these techniques cannot handle specifications that correctly characterise systems with stochastic behaviour, which occur commonly in reinforcement learning and formal verification. We consider the passive learning problem of inferring a Boolean combination of probabilistic LTL (PLTL) formulas from a set of Markov chains, classified as either positive or negative. We propose a novel learning algorithm that infers concise PLTL specifications, leveraging grammar-based enumeration, search heuristics, probabilistic model checking and Boolean set-cover procedures. We demonstrate the effectiveness of our algorithm in two use cases: learning from policies induced by RL algorithms and learning from variants of a probabilistic model. In both cases, our method automatically and efficiently extracts PLTL specifications that succinctly characterise the temporal differences between the policies or model variants.

Efficiently Supporting Hierarchy and Data Updates in DNA Storage

We propose a novel and flexible DNA-storage architecture that provides the notion of hierarchy among the objects tagged with the same primer pair and enables efficient data updates. In contrast to prior work, in our architecture a pair of PCR primers of length 20 does not define a single object, but an independent storage partition, which is internally managed in an independent way with its own index structure. We make the observation that, while the number of mutually compatible primer pairs is limited, the internal address space available to any pair of primers (i.e., partition) is virtually unlimited. We expose and leverage the flexibility with which this address space can be managed to provide rich and functional storage semantics, such as hierarchical data organization and efficient and flexible implementations of data updates. Furthermore, to leverage the full power of the prefix-based nature of PCR addressing, we define a methodology for transforming an arbitrary indexing scheme into a PCR-compatible equivalent. This allows us to run PCR with primers that can be variably extended to include a desired part of the index, and thus narrow down the scope of the reaction to retrieve a specific object (e.g., file or directory) within the partition with high precision. Our wetlab evaluation demonstrates the practicality of the proposed ideas and shows 140x reduction in sequencing cost retrieval of smaller objects within the partition.

Partition Function Estimation: A Quantitative Study

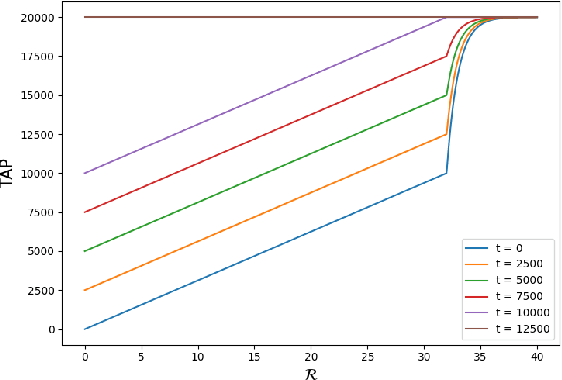
Probabilistic graphical models have emerged as a powerful modeling tool for several real-world scenarios where one needs to reason under uncertainty. A graphical model's partition function is a central quantity of interest, and its computation is key to several probabilistic reasoning tasks. Given the #P-hardness of computing the partition function, several techniques have been proposed over the years with varying guarantees on the quality of estimates and their runtime behavior. This paper seeks to present a survey of 18 techniques and a rigorous empirical study of their behavior across an extensive set of benchmarks. Our empirical study draws up a surprising observation: exact techniques are as efficient as the approximate ones, and therefore, we conclude with an optimistic view of opportunities for the design of approximate techniques with enhanced scalability. Motivated by the observation of an order of magnitude difference between the Virtual Best Solver and the best performing tool, we envision an exciting line of research focused on the development of portfolio solvers.

Phase Transition Behavior of Cardinality and XOR Constraints

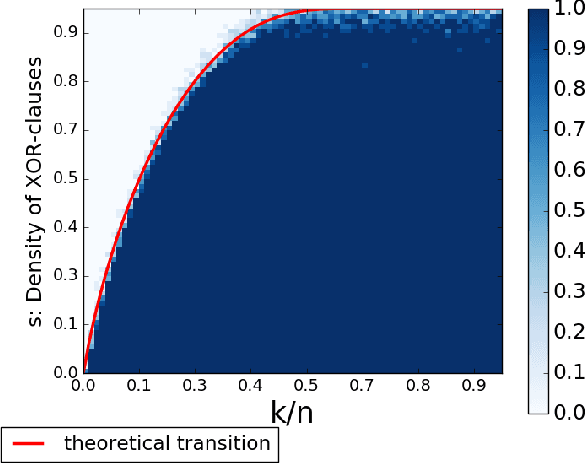
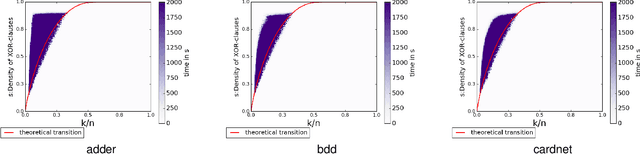
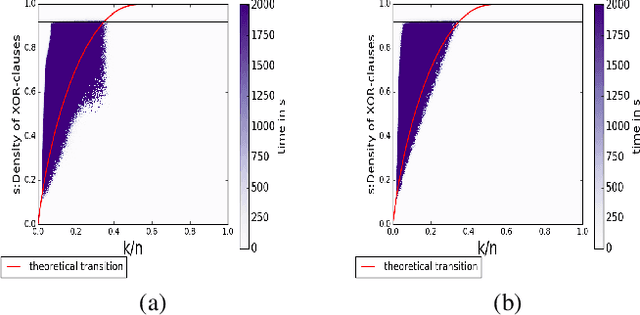
The runtime performance of modern SAT solvers is deeply connected to the phase transition behavior of CNF formulas. While CNF solving has witnessed significant runtime improvement over the past two decades, the same does not hold for several other classes such as the conjunction of cardinality and XOR constraints, denoted as CARD-XOR formulas. The problem of determining the satisfiability of CARD-XOR formulas is a fundamental problem with a wide variety of applications ranging from discrete integration in the field of artificial intelligence to maximum likelihood decoding in coding theory. The runtime behavior of random CARD-XOR formulas is unexplored in prior work. In this paper, we present the first rigorous empirical study to characterize the runtime behavior of 1-CARD-XOR formulas. We show empirical evidence of a surprising phase-transition that follows a non-linear tradeoff between CARD and XOR constraints.