Phase Transition Behavior of Cardinality and XOR Constraints

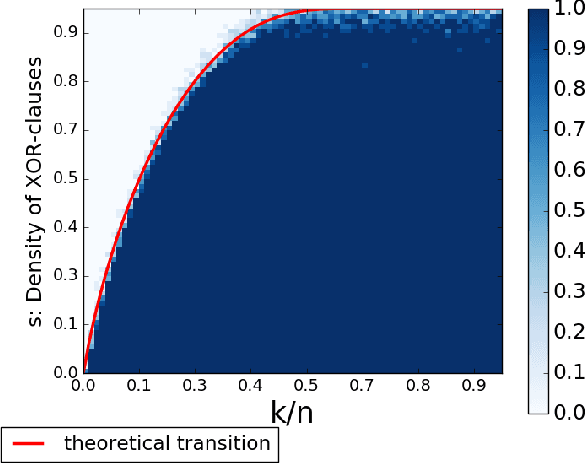
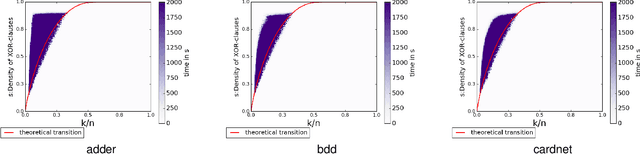
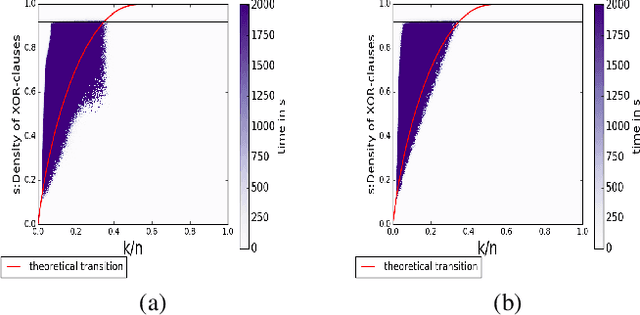
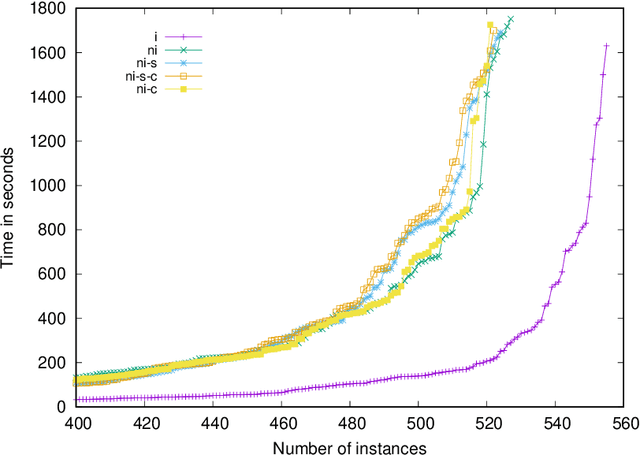
The runtime performance of modern SAT solvers is deeply connected to the phase transition behavior of CNF formulas. While CNF solving has witnessed significant runtime improvement over the past two decades, the same does not hold for several other classes such as the conjunction of cardinality and XOR constraints, denoted as CARD-XOR formulas. The problem of determining the satisfiability of CARD-XOR formulas is a fundamental problem with a wide variety of applications ranging from discrete integration in the field of artificial intelligence to maximum likelihood decoding in coding theory. The runtime behavior of random CARD-XOR formulas is unexplored in prior work. In this paper, we present the first rigorous empirical study to characterize the runtime behavior of 1-CARD-XOR formulas. We show empirical evidence of a surprising phase-transition that follows a non-linear tradeoff between CARD and XOR constraints.

Reflections on "Incremental Cardinality Constraints for MaxSAT"

To celebrate the first 25 years of the International Conference on Principles and Practice of Constraint Programming (CP) the editors invited the authors of the most cited paper of each year to write a commentary on their paper. This report describes our reflections on the CP 2014 paper "Incremental Cardinality Constraints for MaxSAT" and its impact on the Maximum Satisfiability community and beyond.

Approximation Strategies for Incomplete MaxSAT

Incomplete MaxSAT solving aims to quickly find a solution that attempts to minimize the sum of the weights of the unsatisfied soft clauses without providing any optimality guarantees. In this paper, we propose two approximation strategies for improving incomplete MaxSAT solving. In one of the strategies, we cluster the weights and approximate them with a representative weight. In another strategy, we break up the problem of minimizing the sum of weights of unsatisfiable clauses into multiple minimization subproblems. Experimental results show that approximation strategies can be used to find better solutions than the best incomplete solvers in the MaxSAT Evaluation 2017.

Generalized Totalizer Encoding for Pseudo-Boolean Constraints

Pseudo-Boolean constraints, also known as 0-1 Integer Linear Constraints, are used to model many real-world problems. A common approach to solve these constraints is to encode them into a SAT formula. The runtime of the SAT solver on such formula is sensitive to the manner in which the given pseudo-Boolean constraints are encoded. In this paper, we propose generalized Totalizer encoding (GTE), which is an arc-consistency preserving extension of the Totalizer encoding to pseudo-Boolean constraints. Unlike some other encodings, the number of auxiliary variables required for GTE does not depend on the magnitudes of the coefficients. Instead, it depends on the number of distinct combinations of these coefficients. We show the superiority of GTE with respect to other encodings when large pseudo-Boolean constraints have low number of distinct coefficients. Our experimental results also show that GTE remains competitive even when the pseudo-Boolean constraints do not have this characteristic.

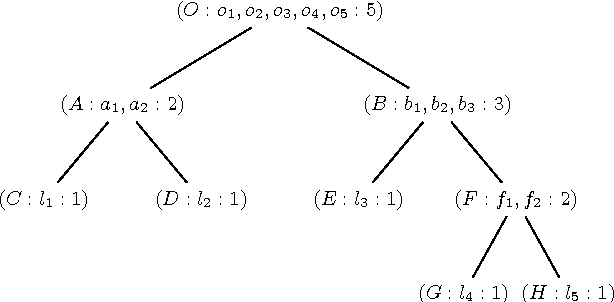
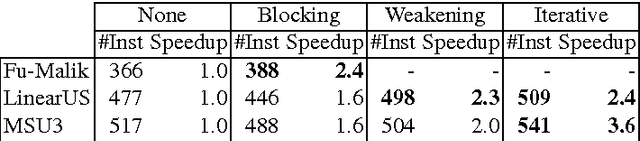
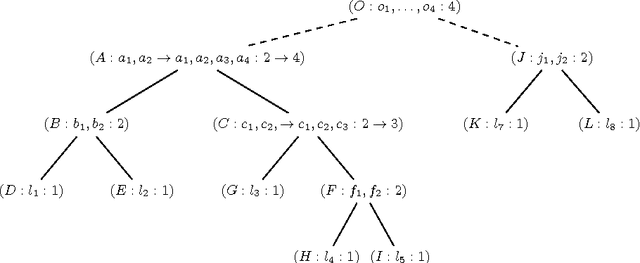
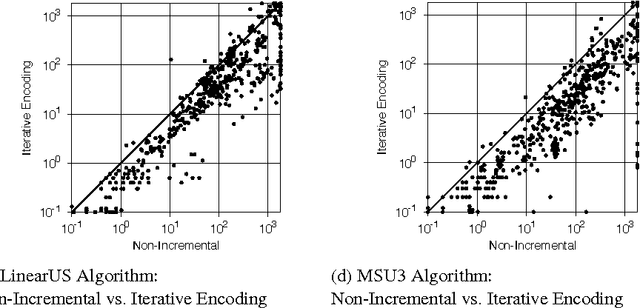
Incremental Cardinality Constraints for MaxSAT

Maximum Satisfiability (MaxSAT) is an optimization variant of the Boolean Satisfiability (SAT) problem. In general, MaxSAT algorithms perform a succession of SAT solver calls to reach an optimum solution making extensive use of cardinality constraints. Many of these algorithms are non-incremental in nature, i.e. at each iteration the formula is rebuilt and no knowledge is reused from one iteration to another. In this paper, we exploit the knowledge acquired across iterations using novel schemes to use cardinality constraints in an incremental fashion. We integrate these schemes with several MaxSAT algorithms. Our experimental results show a significant performance boost for these algo- rithms as compared to their non-incremental counterparts. These results suggest that incremental cardinality constraints could be beneficial for other constraint solving domains.