Incremental Cardinality Constraints for MaxSAT
Paper and Code
Aug 20, 2014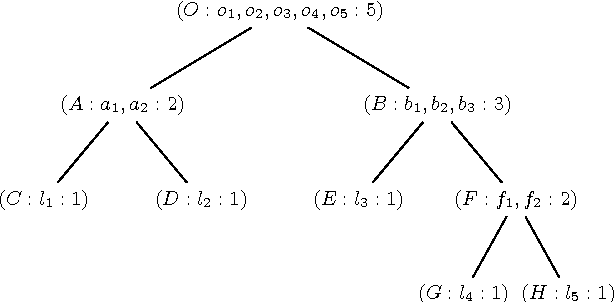
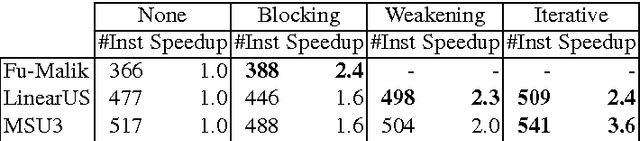
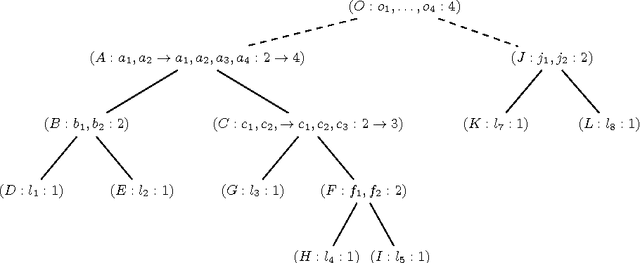
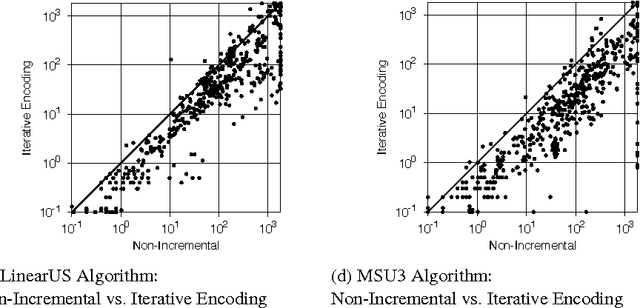
Maximum Satisfiability (MaxSAT) is an optimization variant of the Boolean Satisfiability (SAT) problem. In general, MaxSAT algorithms perform a succession of SAT solver calls to reach an optimum solution making extensive use of cardinality constraints. Many of these algorithms are non-incremental in nature, i.e. at each iteration the formula is rebuilt and no knowledge is reused from one iteration to another. In this paper, we exploit the knowledge acquired across iterations using novel schemes to use cardinality constraints in an incremental fashion. We integrate these schemes with several MaxSAT algorithms. Our experimental results show a significant performance boost for these algo- rithms as compared to their non-incremental counterparts. These results suggest that incremental cardinality constraints could be beneficial for other constraint solving domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge