Reflections on "Incremental Cardinality Constraints for MaxSAT"

To celebrate the first 25 years of the International Conference on Principles and Practice of Constraint Programming (CP) the editors invited the authors of the most cited paper of each year to write a commentary on their paper. This report describes our reflections on the CP 2014 paper "Incremental Cardinality Constraints for MaxSAT" and its impact on the Maximum Satisfiability community and beyond.

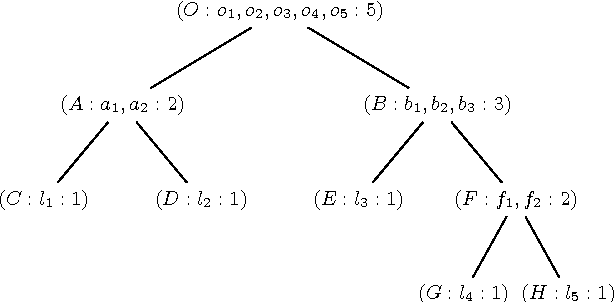
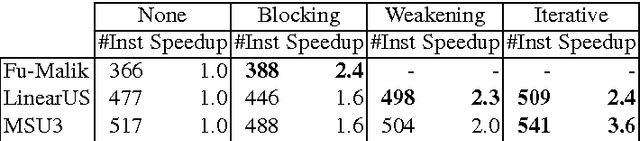
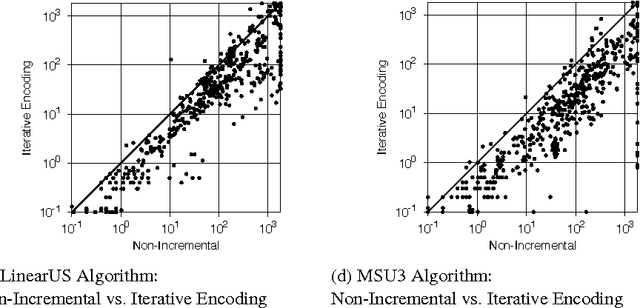
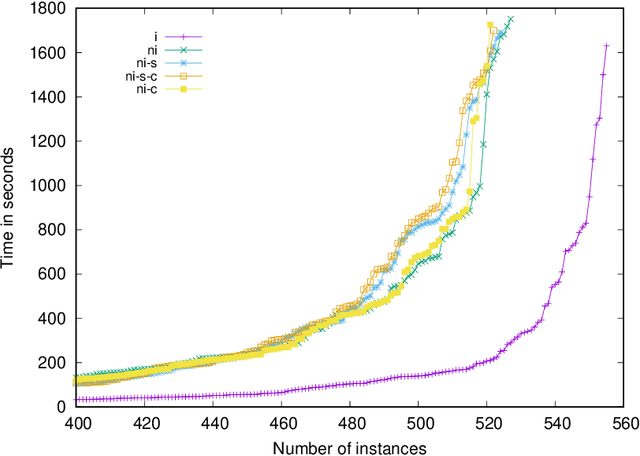
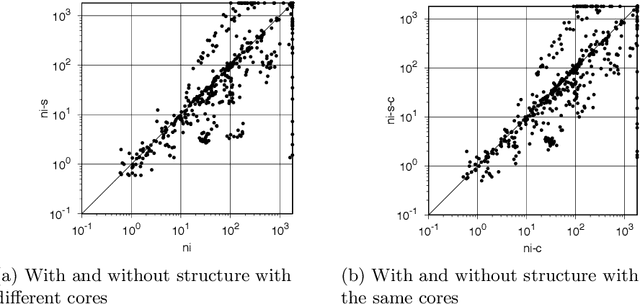
Incremental Cardinality Constraints for MaxSAT

Maximum Satisfiability (MaxSAT) is an optimization variant of the Boolean Satisfiability (SAT) problem. In general, MaxSAT algorithms perform a succession of SAT solver calls to reach an optimum solution making extensive use of cardinality constraints. Many of these algorithms are non-incremental in nature, i.e. at each iteration the formula is rebuilt and no knowledge is reused from one iteration to another. In this paper, we exploit the knowledge acquired across iterations using novel schemes to use cardinality constraints in an incremental fashion. We integrate these schemes with several MaxSAT algorithms. Our experimental results show a significant performance boost for these algo- rithms as compared to their non-incremental counterparts. These results suggest that incremental cardinality constraints could be beneficial for other constraint solving domains.

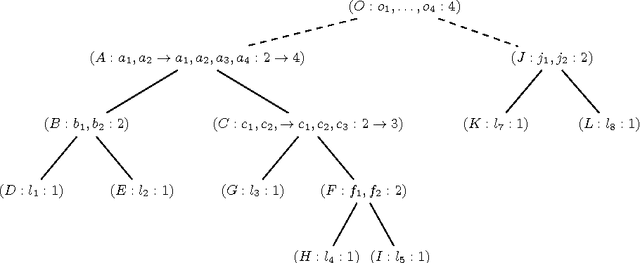
On Solving Boolean Multilevel Optimization Problems

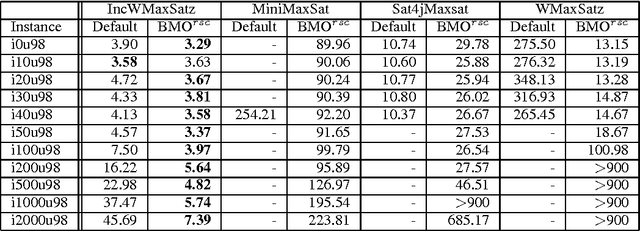
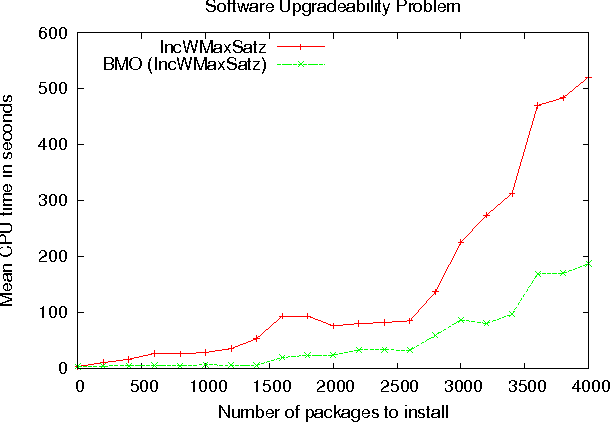
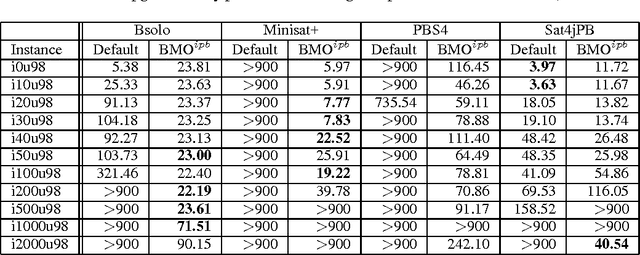
Many combinatorial optimization problems entail a number of hierarchically dependent optimization problems. An often used solution is to associate a suitably large cost with each individual optimization problem, such that the solution of the resulting aggregated optimization problem solves the original set of hierarchically dependent optimization problems. This paper starts by studying the package upgradeability problem in software distributions. Straightforward solutions based on Maximum Satisfiability (MaxSAT) and pseudo-Boolean (PB) optimization are shown to be ineffective, and unlikely to scale for large problem instances. Afterwards, the package upgradeability problem is related to multilevel optimization. The paper then develops new algorithms for Boolean Multilevel Optimization (BMO) and highlights a large number of potential applications. The experimental results indicate that the proposed algorithms for BMO allow solving optimization problems that existing MaxSAT and PB solvers would otherwise be unable to solve.

Symmetry Breaking for Maximum Satisfiability

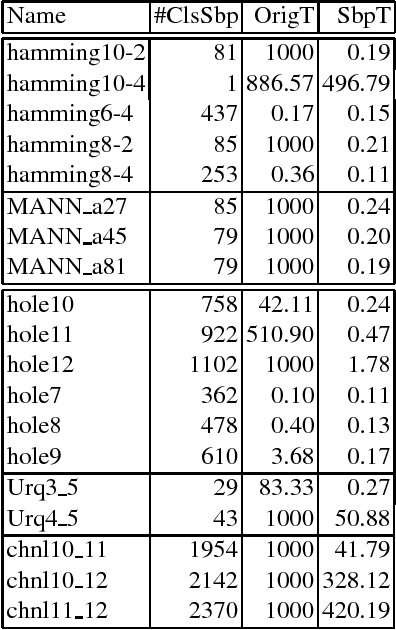
Symmetries are intrinsic to many combinatorial problems including Boolean Satisfiability (SAT) and Constraint Programming (CP). In SAT, the identification of symmetry breaking predicates (SBPs) is a well-known, often effective, technique for solving hard problems. The identification of SBPs in SAT has been the subject of significant improvements in recent years, resulting in more compact SBPs and more effective algorithms. The identification of SBPs has also been applied to pseudo-Boolean (PB) constraints, showing that symmetry breaking can also be an effective technique for PB constraints. This paper extends further the application of SBPs, and shows that SBPs can be identified and used in Maximum Satisfiability (MaxSAT), as well as in its most well-known variants, including partial MaxSAT, weighted MaxSAT and weighted partial MaxSAT. As with SAT and PB, symmetry breaking predicates for MaxSAT and variants are shown to be effective for a representative number of problem domains, allowing solving problem instances that current state of the art MaxSAT solvers could not otherwise solve.