Symmetry Breaking for Maximum Satisfiability
Paper and Code
Apr 03, 2008


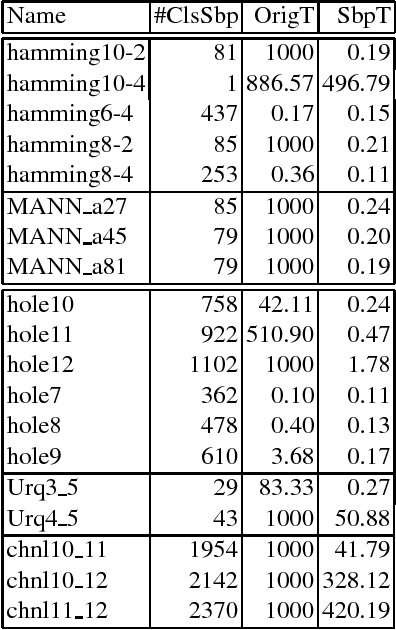
Symmetries are intrinsic to many combinatorial problems including Boolean Satisfiability (SAT) and Constraint Programming (CP). In SAT, the identification of symmetry breaking predicates (SBPs) is a well-known, often effective, technique for solving hard problems. The identification of SBPs in SAT has been the subject of significant improvements in recent years, resulting in more compact SBPs and more effective algorithms. The identification of SBPs has also been applied to pseudo-Boolean (PB) constraints, showing that symmetry breaking can also be an effective technique for PB constraints. This paper extends further the application of SBPs, and shows that SBPs can be identified and used in Maximum Satisfiability (MaxSAT), as well as in its most well-known variants, including partial MaxSAT, weighted MaxSAT and weighted partial MaxSAT. As with SAT and PB, symmetry breaking predicates for MaxSAT and variants are shown to be effective for a representative number of problem domains, allowing solving problem instances that current state of the art MaxSAT solvers could not otherwise solve.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge