On the Complexity of the Bipartite Polarization Problem: from Neutral to Highly Polarized Discussions

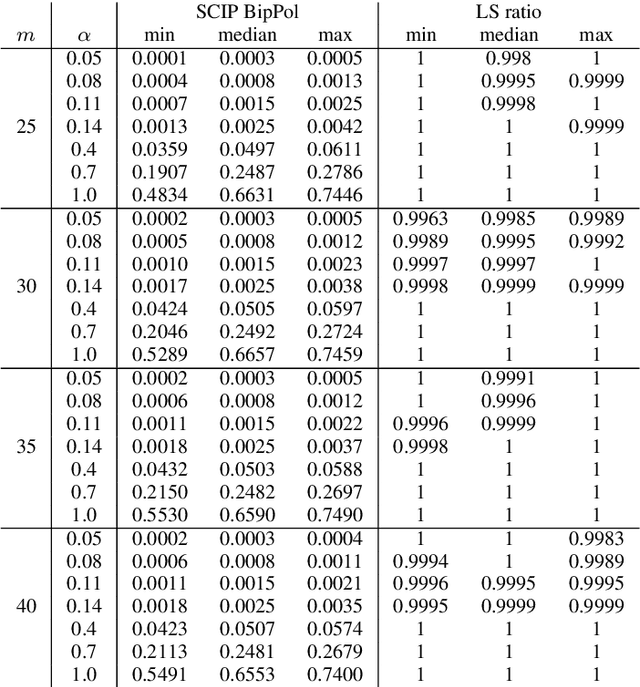
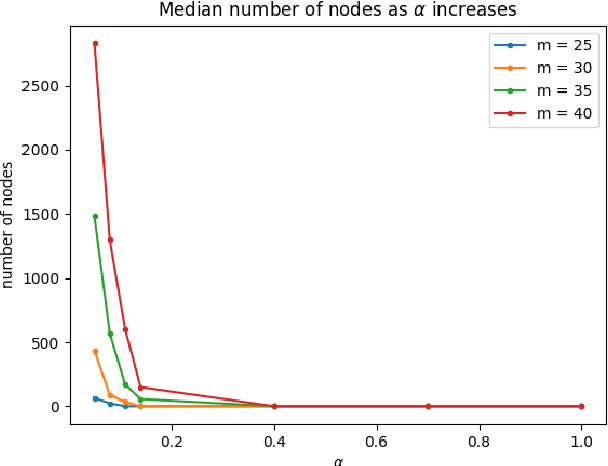
The Bipartite Polarization Problem is an optimization problem where the goal is to find the highest polarized bipartition on a weighted and labelled graph that represents a debate developed through some social network, where nodes represent user's opinions and edges agreement or disagreement between users. This problem can be seen as a generalization of the maxcut problem, and in previous work approximate solutions and exact solutions have been obtained for real instances obtained from Reddit discussions, showing that such real instances seem to be very easy to solve. In this paper, we investigate further the complexity of this problem, by introducing an instance generation model where a single parameter controls the polarization of the instances in such a way that this correlates with the average complexity to solve those instances. The average complexity results we obtain are consistent with our hypothesis: the higher the polarization of the instance, the easier is to find the corresponding polarized bipartition.

On Solving Boolean Multilevel Optimization Problems

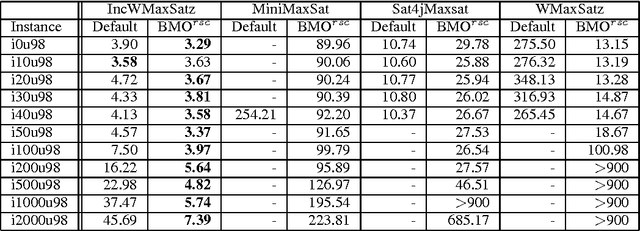
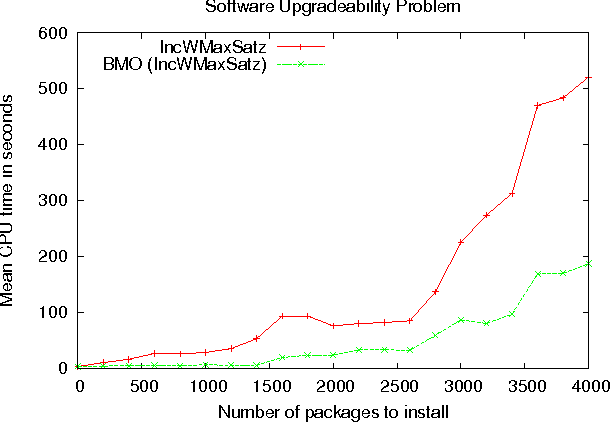
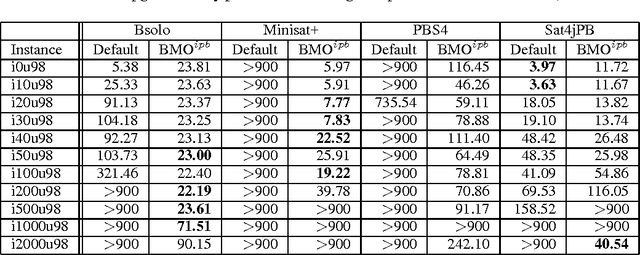
Many combinatorial optimization problems entail a number of hierarchically dependent optimization problems. An often used solution is to associate a suitably large cost with each individual optimization problem, such that the solution of the resulting aggregated optimization problem solves the original set of hierarchically dependent optimization problems. This paper starts by studying the package upgradeability problem in software distributions. Straightforward solutions based on Maximum Satisfiability (MaxSAT) and pseudo-Boolean (PB) optimization are shown to be ineffective, and unlikely to scale for large problem instances. Afterwards, the package upgradeability problem is related to multilevel optimization. The paper then develops new algorithms for Boolean Multilevel Optimization (BMO) and highlights a large number of potential applications. The experimental results indicate that the proposed algorithms for BMO allow solving optimization problems that existing MaxSAT and PB solvers would otherwise be unable to solve.