Phase Transition Behavior in Knowledge Compilation
Paper and Code
Jul 20, 2020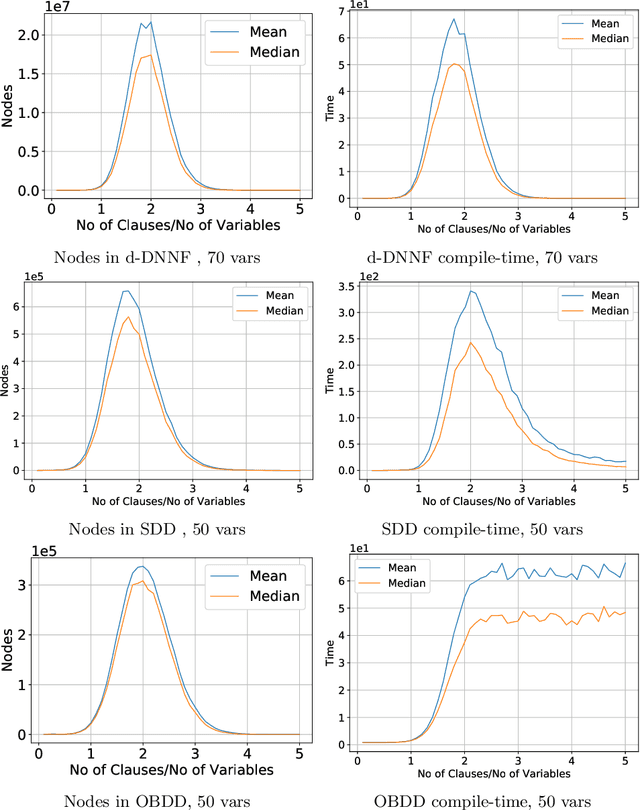
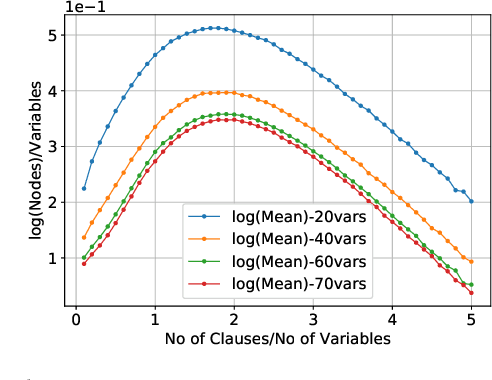
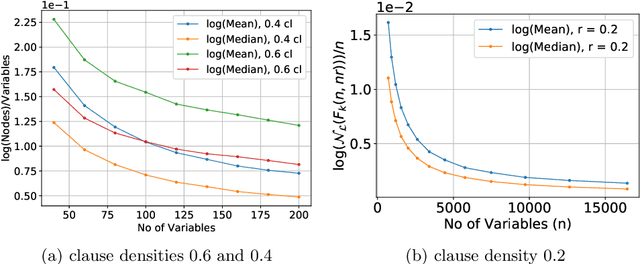
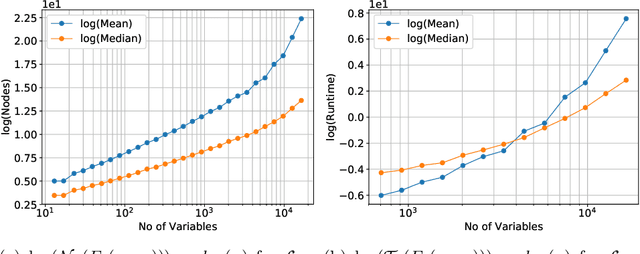
The study of phase transition behaviour in SAT has led to deeper understanding and algorithmic improvements of modern SAT solvers. Motivated by these prior studies of phase transitions in SAT, we seek to study the behaviour of size and compile-time behaviour for random k-CNF formulas in the context of knowledge compilation. We perform a rigorous empirical study and analysis of the size and runtime behavior for different knowledge compilation forms (and their corresponding compilation algorithms): d-DNNFs, SDDs and OBDDs across multiple tools and compilation algorithms. We employ instances generated from the random k-CNF model with varying generation parameters to empirically reason about the expected and median behavior of size and compilation-time for these languages. Our work is similar in spirit to the early work in CSP community on phase transition behavior in SAT/CSP. In a similar spirit, we identify the interesting behavior with respect to different parameters: clause density and solution density, a novel control parameter that we identify for the study of phase transition behavior in the context of knowledge compilation. Furthermore, we summarize our empirical study in terms of two concrete conjectures; a rigorous study of these conjectures will possibly require new theoretical tools.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge