Engineering an Efficient Boolean Functional Synthesis Engine

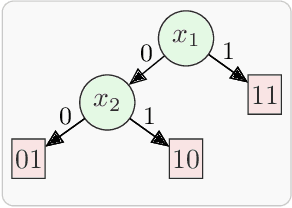
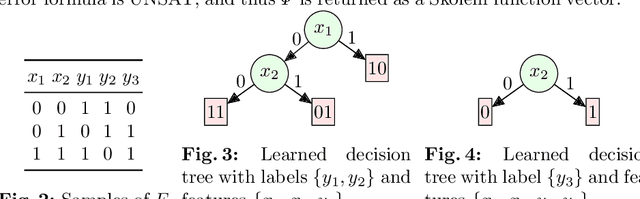
Given a Boolean specification between a set of inputs and outputs, the problem of Boolean functional synthesis is to synthesise each output as a function of inputs such that the specification is met. Although the past few years have witnessed intense algorithmic development, accomplishing scalability remains the holy grail. The state-of-the-art approach combines machine learning and automated reasoning to efficiently synthesise Boolean functions. In this paper, we propose four algorithmic improvements for a data-driven framework for functional synthesis: using a dependency-driven multi-classifier to learn candidate function, extracting uniquely defined functions by interpolation, variables retention, and using lexicographic MaxSAT to repair candidates. We implement these improvements in the state-of-the-art framework, called Manthan. The proposed framework is called Manthan2. Manthan2 shows significantly improved runtime performance compared to Manthan. In an extensive experimental evaluation on 609 benchmarks, Manthan2 is able to synthesise a Boolean function vector for 509 instances compared to 356 instances solved by Manthan--- an increment of 153 instances over the state-of-the-art. To put this into perspective, Manthan improved on the prior state-of-the-art by only 76 instances.

Proof Complexity of Symbolic QBF Reasoning

We introduce and investigate symbolic proof systems for Quantified Boolean Formulas (QBF) operating on Ordered Binary Decision Diagrams (OBDDs). These systems capture QBF solvers that perform symbolic quantifier elimination, and as such admit short proofs of formulas of bounded path-width and quantifier complexity. As a consequence, we obtain exponential separations from standard clausal proof systems, specifically (long-distance) QU-Resolution and IR-Calc. We further develop a lower bound technique for symbolic QBF proof systems based on strategy extraction that lifts known lower bounds from communication complexity. This allows us to derive strong lower bounds against symbolic QBF proof systems that are independent of the variable ordering of the underlying OBDDs, and that hold even if the proof system is allowed access to an NP-oracle.