Moment Multicalibration for Uncertainty Estimation

We show how to achieve the notion of "multicalibration" from H\'ebert-Johnson et al. [2018] not just for means, but also for variances and other higher moments. Informally, it means that we can find regression functions which, given a data point, can make point predictions not just for the expectation of its label, but for higher moments of its label distribution as well-and those predictions match the true distribution quantities when averaged not just over the population as a whole, but also when averaged over an enormous number of finely defined subgroups. It yields a principled way to estimate the uncertainty of predictions on many different subgroups-and to diagnose potential sources of unfairness in the predictive power of features across subgroups. As an application, we show that our moment estimates can be used to derive marginal prediction intervals that are simultaneously valid as averaged over all of the (sufficiently large) subgroups for which moment multicalibration has been obtained.

Fair Prediction with Endogenous Behavior

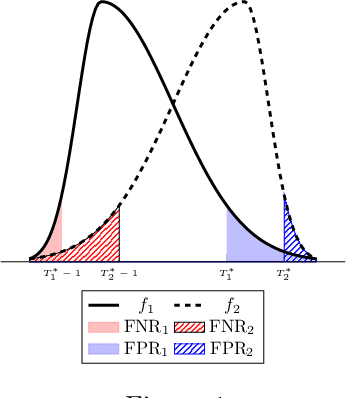
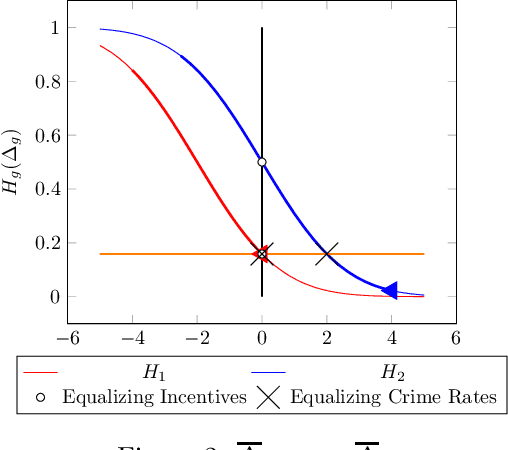
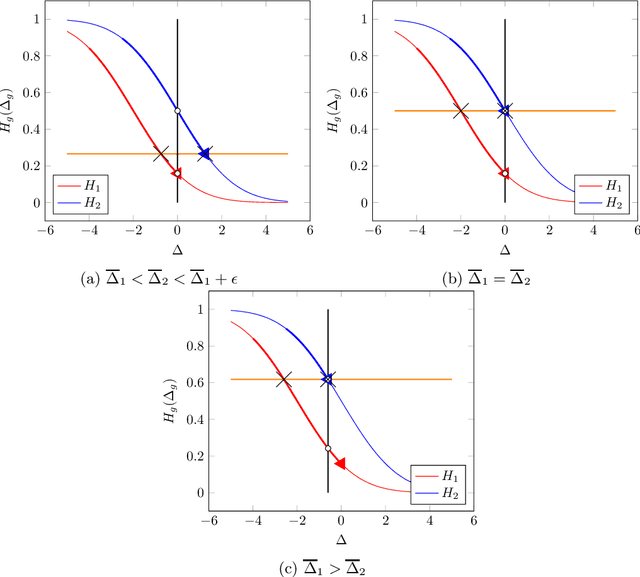
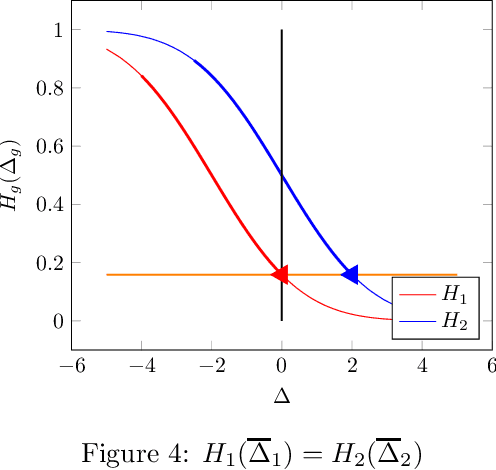
There is increasing regulatory interest in whether machine learning algorithms deployed in consequential domains (e.g. in criminal justice) treat different demographic groups "fairly." However, there are several proposed notions of fairness, typically mutually incompatible. Using criminal justice as an example, we study a model in which society chooses an incarceration rule. Agents of different demographic groups differ in their outside options (e.g. opportunity for legal employment) and decide whether to commit crimes. We show that equalizing type I and type II errors across groups is consistent with the goal of minimizing the overall crime rate; other popular notions of fairness are not.

Do Prices Coordinate Markets?

Walrasian equilibrium prices can be said to coordinate markets: They support a welfare optimal allocation in which each buyer is buying bundle of goods that is individually most preferred. However, this clean story has two caveats. First, the prices alone are not sufficient to coordinate the market, and buyers may need to select among their most preferred bundles in a coordinated way to find a feasible allocation. Second, we don't in practice expect to encounter exact equilibrium prices tailored to the market, but instead only approximate prices, somehow encoding "distributional" information about the market. How well do prices work to coordinate markets when tie-breaking is not coordinated, and they encode only distributional information? We answer this question. First, we provide a genericity condition such that for buyers with Matroid Based Valuations, overdemand with respect to equilibrium prices is at most 1, independent of the supply of goods, even when tie-breaking is done in an uncoordinated fashion. Second, we provide learning-theoretic results that show that such prices are robust to changing the buyers in the market, so long as all buyers are sampled from the same (unknown) distribution.