Online Multivalid Learning: Means, Moments, and Prediction Intervals

We present a general, efficient technique for providing contextual predictions that are "multivalid" in various senses, against an online sequence of adversarially chosen examples $(x,y)$. This means that the resulting estimates correctly predict various statistics of the labels $y$ not just marginally -- as averaged over the sequence of examples -- but also conditionally on $x \in G$ for any $G$ belonging to an arbitrary intersecting collection of groups $\mathcal{G}$. We provide three instantiations of this framework. The first is mean prediction, which corresponds to an online algorithm satisfying the notion of multicalibration from Hebert-Johnson et al. The second is variance and higher moment prediction, which corresponds to an online algorithm satisfying the notion of mean-conditioned moment multicalibration from Jung et al. Finally, we define a new notion of prediction interval multivalidity, and give an algorithm for finding prediction intervals which satisfy it. Because our algorithms handle adversarially chosen examples, they can equally well be used to predict statistics of the residuals of arbitrary point prediction methods, giving rise to very general techniques for quantifying the uncertainty of predictions of black box algorithms, even in an online adversarial setting. When instantiated for prediction intervals, this solves a similar problem as conformal prediction, but in an adversarial environment and with multivalidity guarantees stronger than simple marginal coverage guarantees.

Moment Multicalibration for Uncertainty Estimation

We show how to achieve the notion of "multicalibration" from H\'ebert-Johnson et al. [2018] not just for means, but also for variances and other higher moments. Informally, it means that we can find regression functions which, given a data point, can make point predictions not just for the expectation of its label, but for higher moments of its label distribution as well-and those predictions match the true distribution quantities when averaged not just over the population as a whole, but also when averaged over an enormous number of finely defined subgroups. It yields a principled way to estimate the uncertainty of predictions on many different subgroups-and to diagnose potential sources of unfairness in the predictive power of features across subgroups. As an application, we show that our moment estimates can be used to derive marginal prediction intervals that are simultaneously valid as averaged over all of the (sufficiently large) subgroups for which moment multicalibration has been obtained.

Fair Prediction with Endogenous Behavior

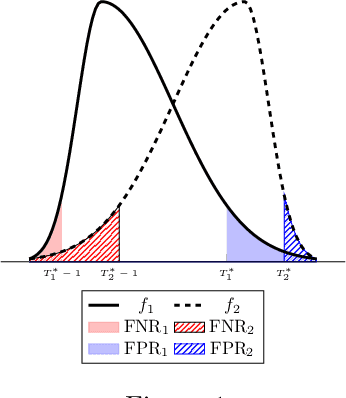
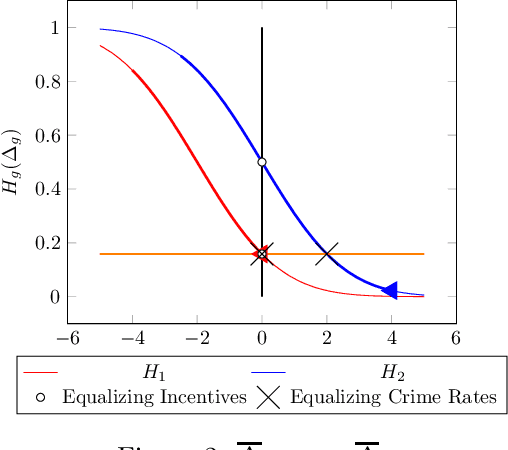
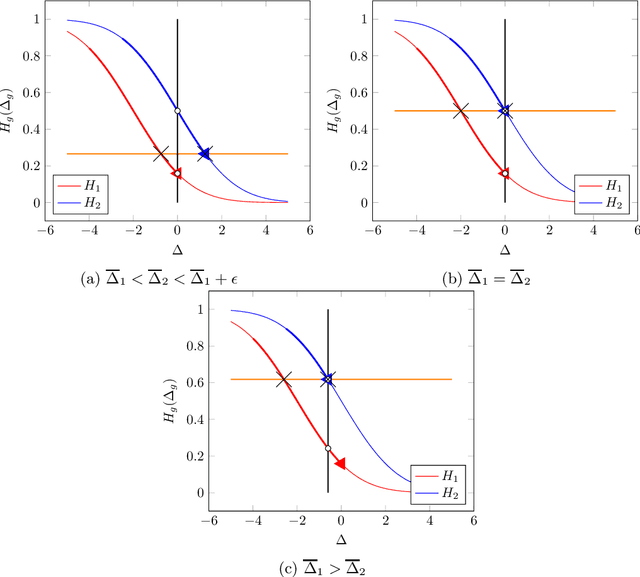
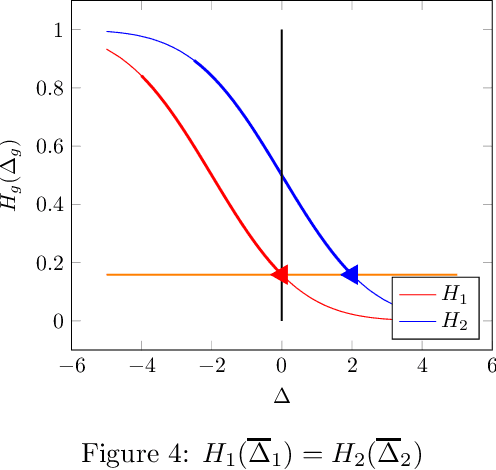
There is increasing regulatory interest in whether machine learning algorithms deployed in consequential domains (e.g. in criminal justice) treat different demographic groups "fairly." However, there are several proposed notions of fairness, typically mutually incompatible. Using criminal justice as an example, we study a model in which society chooses an incarceration rule. Agents of different demographic groups differ in their outside options (e.g. opportunity for legal employment) and decide whether to commit crimes. We show that equalizing type I and type II errors across groups is consistent with the goal of minimizing the overall crime rate; other popular notions of fairness are not.