The Sample Complexity of Multicalibration

We study the minimax sample complexity of multicalibration in the batch setting. A learner observes $n$ i.i.d. samples from an unknown distribution and must output a (possibly randomized) predictor whose population multicalibration error, measured by Expected Calibration Error (ECE), is at most $\varepsilon$ with respect to a given family of groups. For every fixed $κ> 0$, in the regime $|G|\le \varepsilon^{-κ}$, we prove that $\widetildeΘ(\varepsilon^{-3})$ samples are necessary and sufficient, up to polylogarithmic factors. The lower bound holds even for randomized predictors, and the upper bound is realized by a randomized predictor obtained via an online-to-batch reduction. This separates the sample complexity of multicalibration from that of marginal calibration, which scales as $\widetildeΘ(\varepsilon^{-2})$, and shows that mean-ECE multicalibration is as difficult in the batch setting as it is in the online setting, in contrast to marginal calibration which is strictly more difficult in the online setting. In contrast we observe that for $κ= 0$, the sample complexity of multicalibration remains $\widetildeΘ(\varepsilon^{-2})$ exhibiting a sharp threshold phenomenon. More generally, we establish matching upper and lower bounds, up to polylogarithmic factors, for a weighted $L_p$ multicalibration metric for all $1 \le p \le 2$, with optimal exponent $3/p$. We also extend the lower-bound template to a regular class of elicitable properties, and combine it with the online upper bounds of Hu et al. (2025) to obtain matching bounds for calibrating properties including expectiles and bounded-density quantiles.

Statistical Early Stopping for Reasoning Models

While LLMs have seen substantial improvement in reasoning capabilities, they also sometimes overthink, generating unnecessary reasoning steps, particularly under uncertainty, given ill-posed or ambiguous queries. We introduce statistically principled early stopping methods that monitor uncertainty signals during generation to mitigate this issue. Our first approach is parametric: it models inter-arrival times of uncertainty keywords as a renewal process and applies sequential testing for stopping. Our second approach is nonparametric and provides finite-sample guarantees on the probability of halting too early on well-posed queries. We conduct empirical evaluations on reasoning tasks across several domains and models. Our results indicate that uncertainty-aware early stopping can improve both efficiency and reliability in LLM reasoning, and we observe especially significant gains for math reasoning.

Foundations of Top-$k$ Decoding For Language Models

Top-$k$ decoding is a widely used method for sampling from LLMs: at each token, only the largest $k$ next-token-probabilities are kept, and the next token is sampled after re-normalizing them to sum to unity. Top-$k$ and other sampling methods are motivated by the intuition that true next-token distributions are sparse, and the noisy LLM probabilities need to be truncated. However, to our knowledge, a precise theoretical motivation for the use of top-$k$ decoding is missing. In this work, we develop a theoretical framework that both explains and generalizes top-$k$ decoding. We view decoding at a fixed token as the recovery of a sparse probability distribution. We consider \emph{Bregman decoders} obtained by minimizing a separable Bregman divergence (for both the \emph{primal} and \emph{dual} cases) with a sparsity-inducing $\ell_0$ regularization. Despite the combinatorial nature of the objective, we show how to optimize it efficiently for a large class of divergences. We show that the optimal decoding strategies are greedy, and further that the loss function is discretely convex in $k$, so that binary search provably and efficiently finds the optimal $k$. We show that top-$k$ decoding arises as a special case for the KL divergence, and identify new decoding strategies that have distinct behaviors (e.g., non-linearly up-weighting larger probabilities after re-normalization).

Stronger Neyman Regret Guarantees for Adaptive Experimental Design

We study the design of adaptive, sequential experiments for unbiased average treatment effect (ATE) estimation in the design-based potential outcomes setting. Our goal is to develop adaptive designs offering sublinear Neyman regret, meaning their efficiency must approach that of the hindsight-optimal nonadaptive design. Recent work [Dai et al, 2023] introduced ClipOGD, the first method achieving $\widetilde{O}(\sqrt{T})$ expected Neyman regret under mild conditions. In this work, we propose adaptive designs with substantially stronger Neyman regret guarantees. In particular, we modify ClipOGD to obtain anytime $\widetilde{O}(\log T)$ Neyman regret under natural boundedness assumptions. Further, in the setting where experimental units have pre-treatment covariates, we introduce and study a class of contextual "multigroup" Neyman regret guarantees: Given any set of possibly overlapping groups based on the covariates, the adaptive design outperforms each group's best non-adaptive designs. In particular, we develop a contextual adaptive design with $\widetilde{O}(\sqrt{T})$ anytime multigroup Neyman regret. We empirically validate the proposed designs through an array of experiments.

High-Dimensional Prediction for Sequential Decision Making

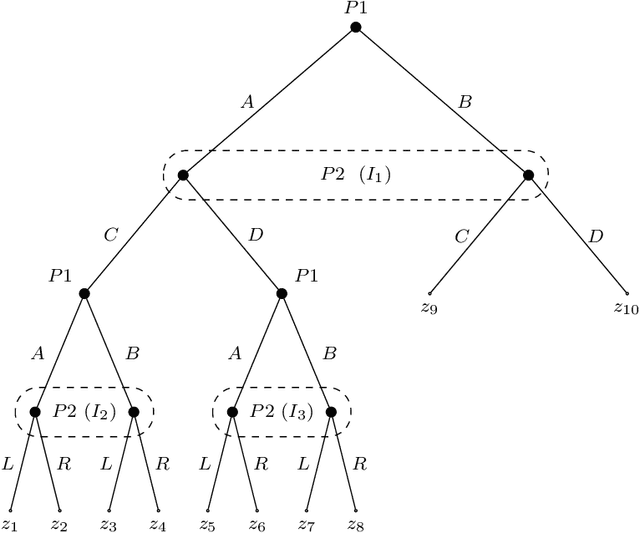
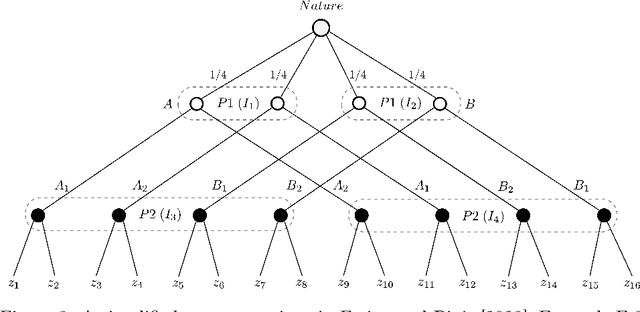
We study the problem of making predictions of an adversarially chosen high-dimensional state that are unbiased subject to an arbitrary collection of conditioning events, with the goal of tailoring these events to downstream decision makers. We give efficient algorithms for solving this problem, as well as a number of applications that stem from choosing an appropriate set of conditioning events. For example, we can efficiently make predictions targeted at polynomially many decision makers, giving each of them optimal swap regret if they best-respond to our predictions. We generalize this to online combinatorial optimization, where the decision makers have a very large action space, to give the first algorithms offering polynomially many decision makers no regret on polynomially many subsequences that may depend on their actions and the context. We apply these results to get efficient no-subsequence-regret algorithms in extensive-form games (EFGs), yielding a new family of regret guarantees for EFGs that generalizes some existing EFG regret notions, e.g. regret to informed causal deviations, and is generally incomparable to other known such notions. Next, we develop a novel transparent alternative to conformal prediction for building valid online adversarial multiclass prediction sets. We produce class scores that downstream algorithms can use for producing valid-coverage prediction sets, as if these scores were the true conditional class probabilities. We show this implies strong conditional validity guarantees including set-size-conditional and multigroup-fair coverage for polynomially many downstream prediction sets. Moreover, our class scores can be guaranteed to have improved $L_2$ loss, cross-entropy loss, and generally any Bregman loss, compared to any collection of benchmark models, yielding a high-dimensional real-valued version of omniprediction.

The Scope of Multicalibration: Characterizing Multicalibration via Property Elicitation

We make a connection between multicalibration and property elicitation and show that (under mild technical conditions) it is possible to produce a multicalibrated predictor for a continuous scalar distributional property $\Gamma$ if and only if $\Gamma$ is elicitable. On the negative side, we show that for non-elicitable continuous properties there exist simple data distributions on which even the true distributional predictor is not calibrated. On the positive side, for elicitable $\Gamma$, we give simple canonical algorithms for the batch and the online adversarial setting, that learn a $\Gamma$-multicalibrated predictor. This generalizes past work on multicalibrated means and quantiles, and in fact strengthens existing online quantile multicalibration results. To further counter-weigh our negative result, we show that if a property $\Gamma^1$ is not elicitable by itself, but is elicitable conditionally on another elicitable property $\Gamma^0$, then there is a canonical algorithm that jointly multicalibrates $\Gamma^1$ and $\Gamma^0$; this generalizes past work on mean-moment multicalibration. Finally, as applications of our theory, we provide novel algorithmic and impossibility results for fair (multicalibrated) risk assessment.

Batch Multivalid Conformal Prediction

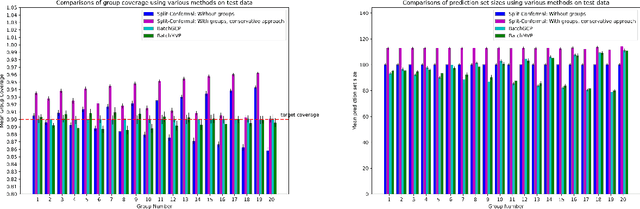
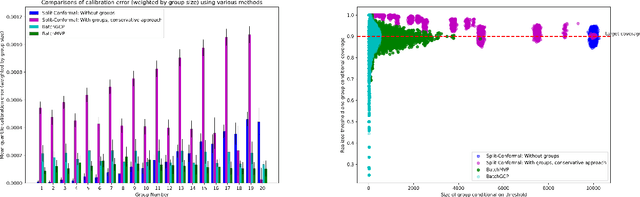
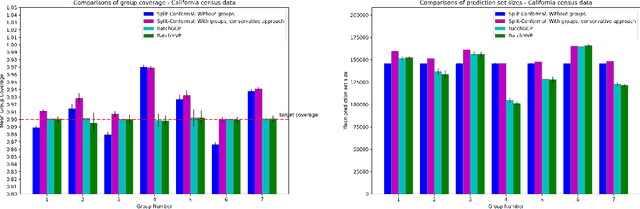
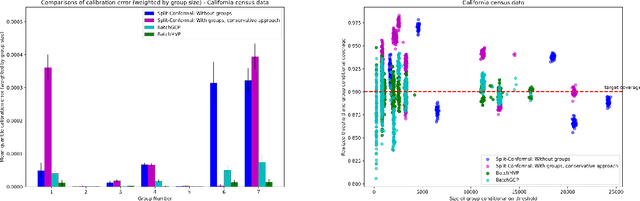
We develop fast distribution-free conformal prediction algorithms for obtaining multivalid coverage on exchangeable data in the batch setting. Multivalid coverage guarantees are stronger than marginal coverage guarantees in two ways: (1) They hold even conditional on group membership -- that is, the target coverage level $1-\alpha$ holds conditionally on membership in each of an arbitrary (potentially intersecting) group in a finite collection $\mathcal{G}$ of regions in the feature space. (2) They hold even conditional on the value of the threshold used to produce the prediction set on a given example. In fact multivalid coverage guarantees hold even when conditioning on group membership and threshold value simultaneously. We give two algorithms: both take as input an arbitrary non-conformity score and an arbitrary collection of possibly intersecting groups $\mathcal{G}$, and then can equip arbitrary black-box predictors with prediction sets. Our first algorithm (BatchGCP) is a direct extension of quantile regression, needs to solve only a single convex minimization problem, and produces an estimator which has group-conditional guarantees for each group in $\mathcal{G}$. Our second algorithm (BatchMVP) is iterative, and gives the full guarantees of multivalid conformal prediction: prediction sets that are valid conditionally both on group membership and non-conformity threshold. We evaluate the performance of both of our algorithms in an extensive set of experiments. Code to replicate all of our experiments can be found at https://github.com/ProgBelarus/BatchMultivalidConformal

Practical Adversarial Multivalid Conformal Prediction

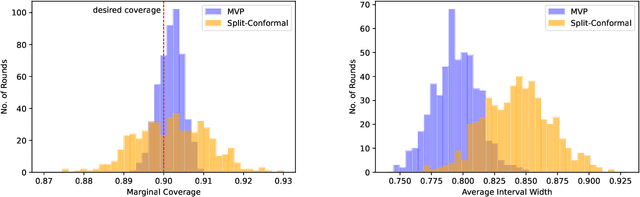
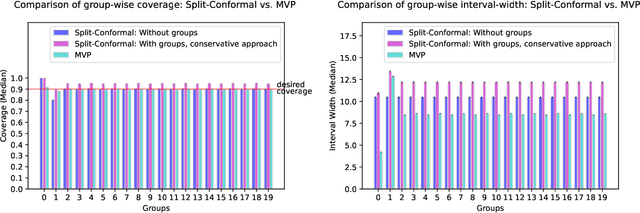
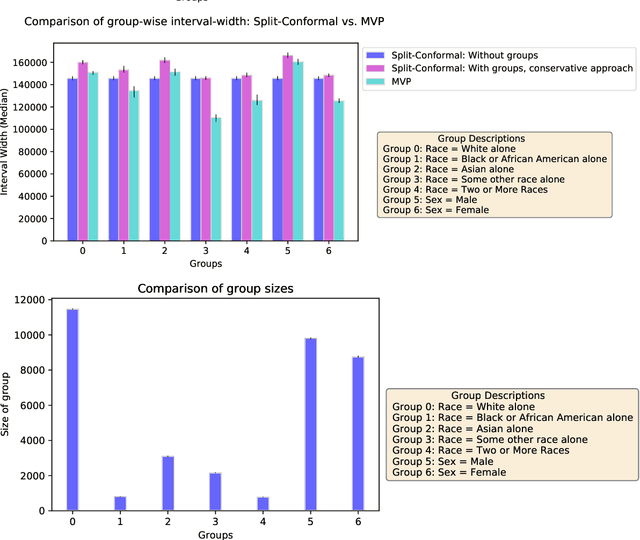
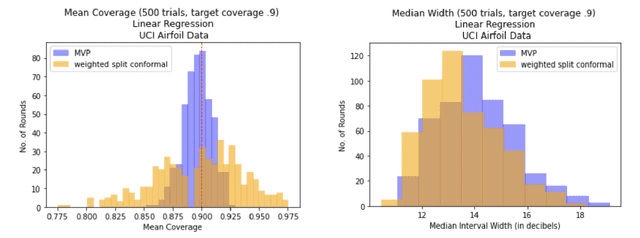
We give a simple, generic conformal prediction method for sequential prediction that achieves target empirical coverage guarantees against adversarially chosen data. It is computationally lightweight -- comparable to split conformal prediction -- but does not require having a held-out validation set, and so all data can be used for training models from which to derive a conformal score. It gives stronger than marginal coverage guarantees in two ways. First, it gives threshold calibrated prediction sets that have correct empirical coverage even conditional on the threshold used to form the prediction set from the conformal score. Second, the user can specify an arbitrary collection of subsets of the feature space -- possibly intersecting -- and the coverage guarantees also hold conditional on membership in each of these subsets. We call our algorithm MVP, short for MultiValid Prediction. We give both theory and an extensive set of empirical evaluations.

Online Multiobjective Minimax Optimization and Applications

We introduce a simple but general online learning framework, in which at every round, an adaptive adversary introduces a new game, consisting of an action space for the learner, an action space for the adversary, and a vector valued objective function that is convex-concave in every coordinate. The learner and the adversary then play in this game. The learner's goal is to play so as to minimize the maximum coordinate of the cumulative vector-valued loss. The resulting one-shot game is not convex-concave, and so the minimax theorem does not apply. Nevertheless, we give a simple algorithm that can compete with the setting in which the adversary must announce their action first, with optimally diminishing regret. We demonstrate the power of our simple framework by using it to derive optimal bounds and algorithms across a variety of domains. This includes no regret learning: we can recover optimal algorithms and bounds for minimizing external regret, internal regret, adaptive regret, multigroup regret, subsequence regret, and a notion of regret in the sleeping experts setting. Next, we use it to derive a variant of Blackwell's Approachability Theorem, which we term "Fast Polytope Approachability". Finally, we are able to recover recently derived algorithms and bounds for online adversarial multicalibration and related notions (mean-conditioned moment multicalibration, and prediction interval multivalidity).

Online Multivalid Learning: Means, Moments, and Prediction Intervals

We present a general, efficient technique for providing contextual predictions that are "multivalid" in various senses, against an online sequence of adversarially chosen examples $(x,y)$. This means that the resulting estimates correctly predict various statistics of the labels $y$ not just marginally -- as averaged over the sequence of examples -- but also conditionally on $x \in G$ for any $G$ belonging to an arbitrary intersecting collection of groups $\mathcal{G}$. We provide three instantiations of this framework. The first is mean prediction, which corresponds to an online algorithm satisfying the notion of multicalibration from Hebert-Johnson et al. The second is variance and higher moment prediction, which corresponds to an online algorithm satisfying the notion of mean-conditioned moment multicalibration from Jung et al. Finally, we define a new notion of prediction interval multivalidity, and give an algorithm for finding prediction intervals which satisfy it. Because our algorithms handle adversarially chosen examples, they can equally well be used to predict statistics of the residuals of arbitrary point prediction methods, giving rise to very general techniques for quantifying the uncertainty of predictions of black box algorithms, even in an online adversarial setting. When instantiated for prediction intervals, this solves a similar problem as conformal prediction, but in an adversarial environment and with multivalidity guarantees stronger than simple marginal coverage guarantees.