A Fast, Reliable, and Secure Programming Language for LLM Agents with Code Actions

Modern large language models (LLMs) are often deployed as agents, calling external tools adaptively to solve tasks. Rather than directly calling tools, it can be more effective for LLMs to write code to perform the tool calls, enabling them to automatically generate complex control flow such as conditionals and loops. Such code actions are typically provided as Python code, since LLMs are quite proficient at it; however, Python may not be the ideal language due to limited built-in support for performance, security, and reliability. We propose a novel programming language for code actions, called Quasar, which has several benefits: (1) automated parallelization to improve performance, (2) uncertainty quantification to improve reliability and mitigate hallucinations, and (3) security features enabling the user to validate actions. LLMs can write code in a subset of Python, which is automatically transpiled to Quasar. We evaluate our approach on the ViperGPT visual question answering agent, applied to the GQA dataset, demonstrating that LLMs with Quasar actions instead of Python actions retain strong performance, while reducing execution time when possible by 42%, improving security by reducing user approval interactions when possible by 52%, and improving reliability by applying conformal prediction to achieve a desired target coverage level.

Uncertainty Quantification for Neurosymbolic Programs via Compositional Conformal Prediction

Machine learning has become an effective tool for automatically annotating unstructured data (e.g., images) with structured labels (e.g., object detections). As a result, a new programming paradigm called neurosymbolic programming has emerged where users write queries against these predicted annotations. However, due to the intrinsic fallibility of machine learning models, these programs currently lack any notion of correctness. In many domains, users may want some kind of conservative guarantee that the results of their queries contain all possibly relevant instances. Conformal prediction has emerged as a promising strategy for quantifying uncertainty in machine learning by modifying models to predict sets of labels instead of individual labels; it provides a probabilistic guarantee that the prediction set contains the true label with high probability. We propose a novel framework for adapting conformal prediction to neurosymbolic programs; our strategy is to represent prediction sets as abstract values in some abstract domain, and then to use abstract interpretation to propagate prediction sets through the program. Our strategy satisfies three key desiderata: (i) correctness (i.e., the program outputs a prediction set that contains the true output with high probability), (ii) compositionality (i.e., we can quantify uncertainty separately for different modules and then compose them together), and (iii) structured values (i.e., we can provide uncertainty quantification for structured values such as lists). When the full program is available ahead-of-time, we propose an optimization that incorporates conformal prediction at intermediate program points to reduce imprecision in abstract interpretation. We evaluate our approach on programs that take MNIST and MS-COCO images as input, demonstrating that it produces reasonably sized prediction sets while satisfying a coverage guarantee.

High-Dimensional Prediction for Sequential Decision Making

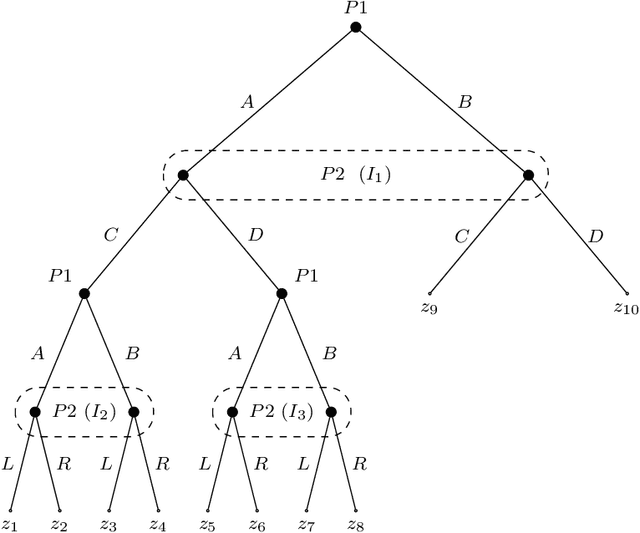
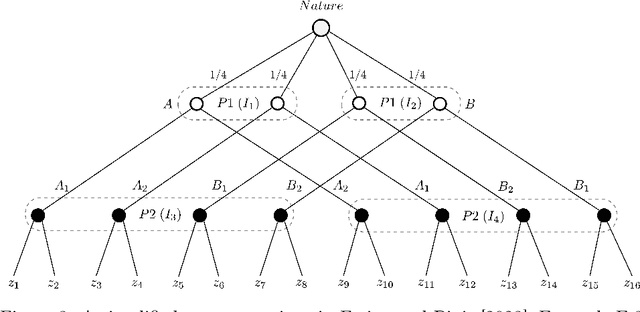
We study the problem of making predictions of an adversarially chosen high-dimensional state that are unbiased subject to an arbitrary collection of conditioning events, with the goal of tailoring these events to downstream decision makers. We give efficient algorithms for solving this problem, as well as a number of applications that stem from choosing an appropriate set of conditioning events. For example, we can efficiently make predictions targeted at polynomially many decision makers, giving each of them optimal swap regret if they best-respond to our predictions. We generalize this to online combinatorial optimization, where the decision makers have a very large action space, to give the first algorithms offering polynomially many decision makers no regret on polynomially many subsequences that may depend on their actions and the context. We apply these results to get efficient no-subsequence-regret algorithms in extensive-form games (EFGs), yielding a new family of regret guarantees for EFGs that generalizes some existing EFG regret notions, e.g. regret to informed causal deviations, and is generally incomparable to other known such notions. Next, we develop a novel transparent alternative to conformal prediction for building valid online adversarial multiclass prediction sets. We produce class scores that downstream algorithms can use for producing valid-coverage prediction sets, as if these scores were the true conditional class probabilities. We show this implies strong conditional validity guarantees including set-size-conditional and multigroup-fair coverage for polynomially many downstream prediction sets. Moreover, our class scores can be guaranteed to have improved $L_2$ loss, cross-entropy loss, and generally any Bregman loss, compared to any collection of benchmark models, yielding a high-dimensional real-valued version of omniprediction.

Batch Multivalid Conformal Prediction

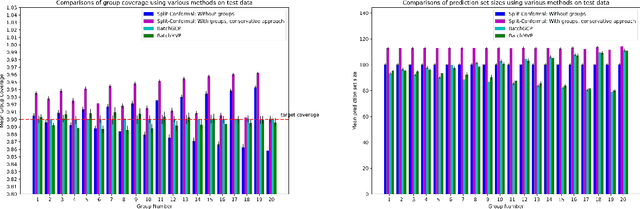
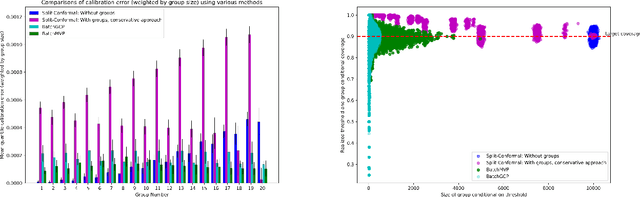
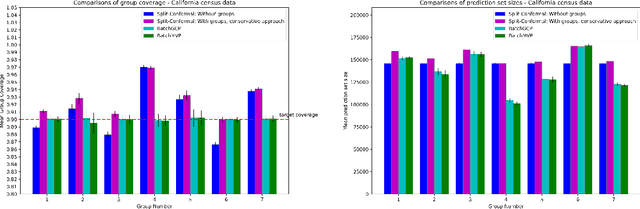
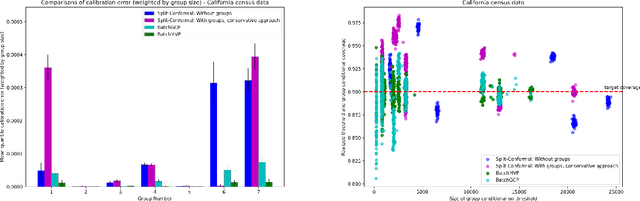
We develop fast distribution-free conformal prediction algorithms for obtaining multivalid coverage on exchangeable data in the batch setting. Multivalid coverage guarantees are stronger than marginal coverage guarantees in two ways: (1) They hold even conditional on group membership -- that is, the target coverage level $1-\alpha$ holds conditionally on membership in each of an arbitrary (potentially intersecting) group in a finite collection $\mathcal{G}$ of regions in the feature space. (2) They hold even conditional on the value of the threshold used to produce the prediction set on a given example. In fact multivalid coverage guarantees hold even when conditioning on group membership and threshold value simultaneously. We give two algorithms: both take as input an arbitrary non-conformity score and an arbitrary collection of possibly intersecting groups $\mathcal{G}$, and then can equip arbitrary black-box predictors with prediction sets. Our first algorithm (BatchGCP) is a direct extension of quantile regression, needs to solve only a single convex minimization problem, and produces an estimator which has group-conditional guarantees for each group in $\mathcal{G}$. Our second algorithm (BatchMVP) is iterative, and gives the full guarantees of multivalid conformal prediction: prediction sets that are valid conditionally both on group membership and non-conformity threshold. We evaluate the performance of both of our algorithms in an extensive set of experiments. Code to replicate all of our experiments can be found at https://github.com/ProgBelarus/BatchMultivalidConformal

Practical Adversarial Multivalid Conformal Prediction

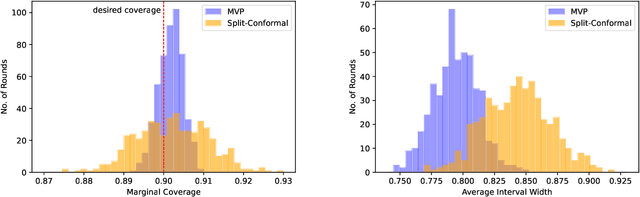
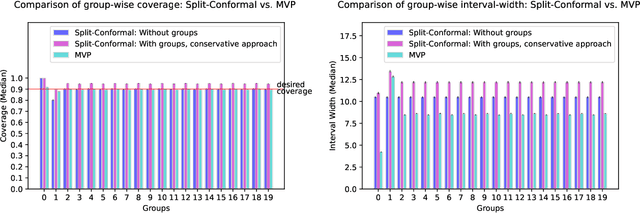
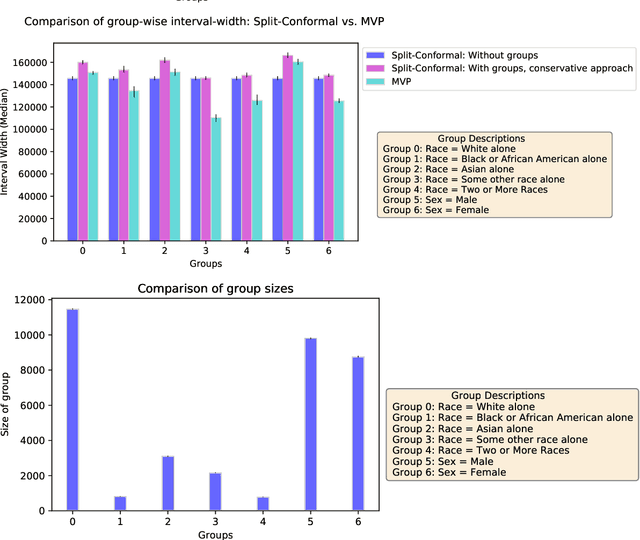
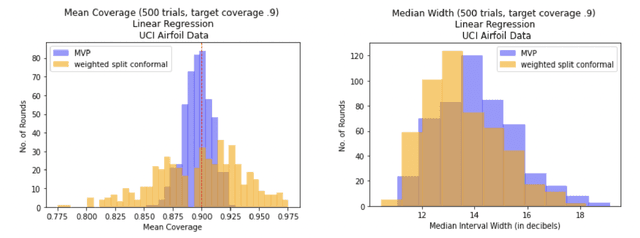
We give a simple, generic conformal prediction method for sequential prediction that achieves target empirical coverage guarantees against adversarially chosen data. It is computationally lightweight -- comparable to split conformal prediction -- but does not require having a held-out validation set, and so all data can be used for training models from which to derive a conformal score. It gives stronger than marginal coverage guarantees in two ways. First, it gives threshold calibrated prediction sets that have correct empirical coverage even conditional on the threshold used to form the prediction set from the conformal score. Second, the user can specify an arbitrary collection of subsets of the feature space -- possibly intersecting -- and the coverage guarantees also hold conditional on membership in each of these subsets. We call our algorithm MVP, short for MultiValid Prediction. We give both theory and an extensive set of empirical evaluations.

Optimized Coverage Planning for UV Surface Disinfection

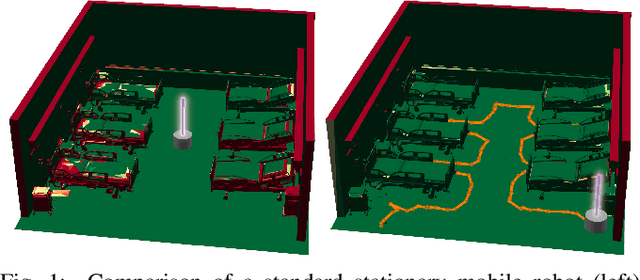
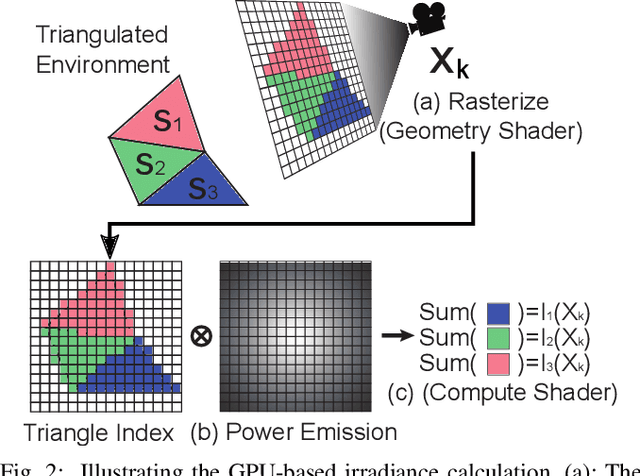
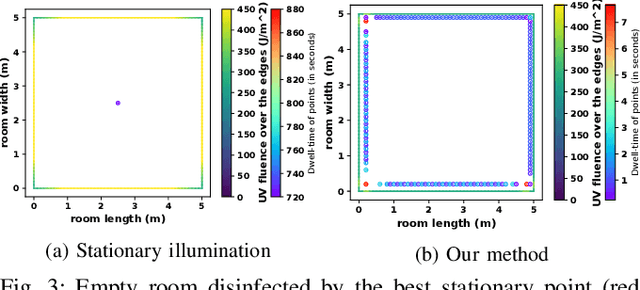
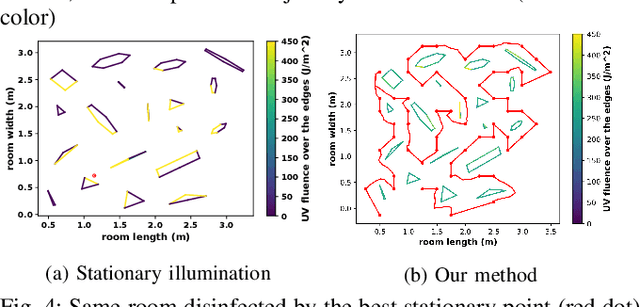
UV radiation has been used as a disinfection strategy to deactivate a wide range of pathogens, but existing irradiation strategies do not ensure sufficient exposure of all environmental surfaces and/or require long disinfection times. We present a near-optimal coverage planner for mobile UV disinfection robots. The formulation optimizes the irradiation time efficiency, while ensuring that a sufficient dosage of radiation is received by each surface. The trajectory and dosage plan are optimized taking collision and light occlusion constraints into account. We propose a two-stage scheme to approximate the solution of the induced NP-hard optimization, and, for efficiency, perform key irradiance and occlusion calculations on a GPU. Empirical results show that our technique achieves more coverage for the same exposure time as strategies for existing UV robots, can be used to compare UV robot designs, and produces near-optimal plans. This is an extended version of the paper originally contributed to ICRA2021.