High-Dimensional Prediction for Sequential Decision Making
Paper and Code
Oct 27, 2023
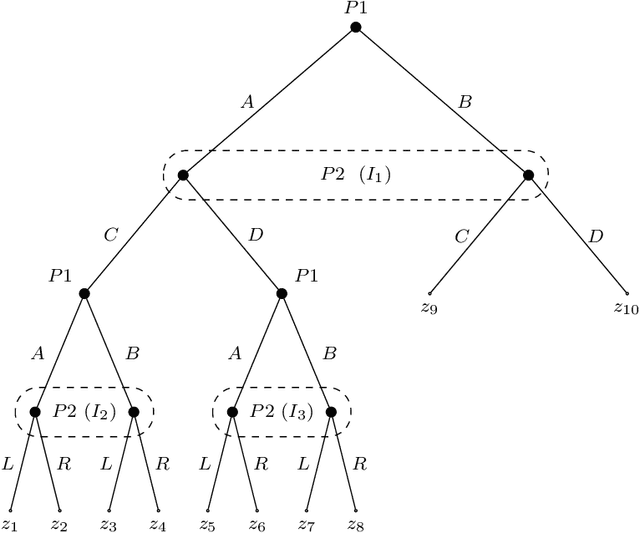
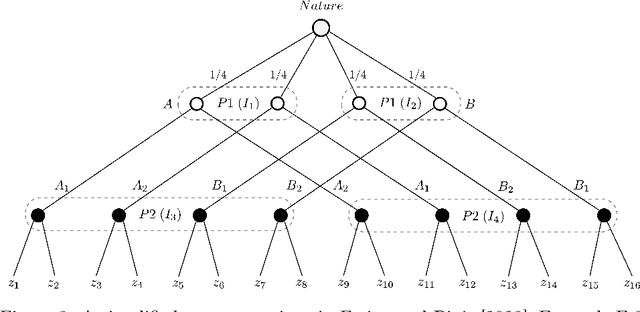
We study the problem of making predictions of an adversarially chosen high-dimensional state that are unbiased subject to an arbitrary collection of conditioning events, with the goal of tailoring these events to downstream decision makers. We give efficient algorithms for solving this problem, as well as a number of applications that stem from choosing an appropriate set of conditioning events. For example, we can efficiently make predictions targeted at polynomially many decision makers, giving each of them optimal swap regret if they best-respond to our predictions. We generalize this to online combinatorial optimization, where the decision makers have a very large action space, to give the first algorithms offering polynomially many decision makers no regret on polynomially many subsequences that may depend on their actions and the context. We apply these results to get efficient no-subsequence-regret algorithms in extensive-form games (EFGs), yielding a new family of regret guarantees for EFGs that generalizes some existing EFG regret notions, e.g. regret to informed causal deviations, and is generally incomparable to other known such notions. Next, we develop a novel transparent alternative to conformal prediction for building valid online adversarial multiclass prediction sets. We produce class scores that downstream algorithms can use for producing valid-coverage prediction sets, as if these scores were the true conditional class probabilities. We show this implies strong conditional validity guarantees including set-size-conditional and multigroup-fair coverage for polynomially many downstream prediction sets. Moreover, our class scores can be guaranteed to have improved $L_2$ loss, cross-entropy loss, and generally any Bregman loss, compared to any collection of benchmark models, yielding a high-dimensional real-valued version of omniprediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge