Batch Multivalid Conformal Prediction
Paper and Code
Sep 30, 2022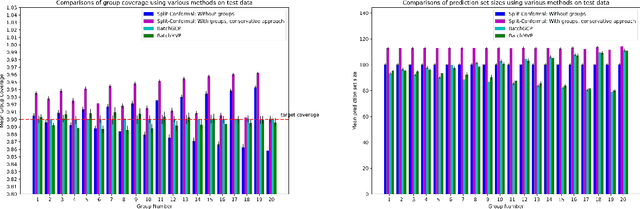
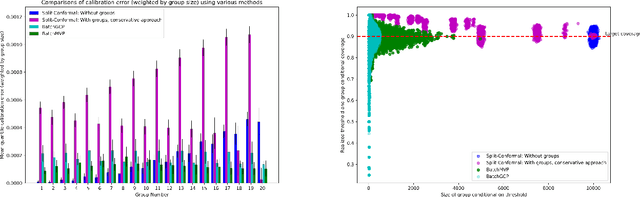
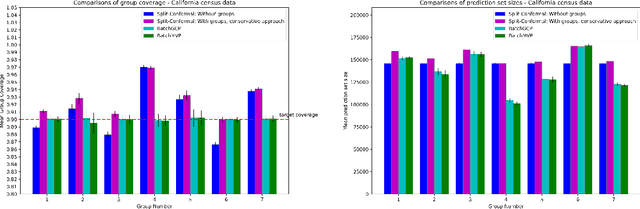
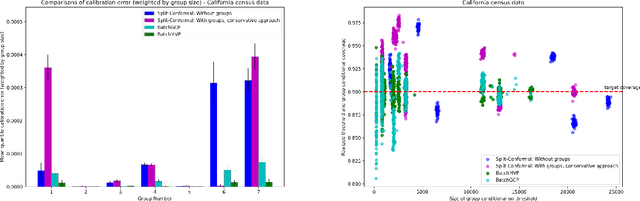
We develop fast distribution-free conformal prediction algorithms for obtaining multivalid coverage on exchangeable data in the batch setting. Multivalid coverage guarantees are stronger than marginal coverage guarantees in two ways: (1) They hold even conditional on group membership -- that is, the target coverage level $1-\alpha$ holds conditionally on membership in each of an arbitrary (potentially intersecting) group in a finite collection $\mathcal{G}$ of regions in the feature space. (2) They hold even conditional on the value of the threshold used to produce the prediction set on a given example. In fact multivalid coverage guarantees hold even when conditioning on group membership and threshold value simultaneously. We give two algorithms: both take as input an arbitrary non-conformity score and an arbitrary collection of possibly intersecting groups $\mathcal{G}$, and then can equip arbitrary black-box predictors with prediction sets. Our first algorithm (BatchGCP) is a direct extension of quantile regression, needs to solve only a single convex minimization problem, and produces an estimator which has group-conditional guarantees for each group in $\mathcal{G}$. Our second algorithm (BatchMVP) is iterative, and gives the full guarantees of multivalid conformal prediction: prediction sets that are valid conditionally both on group membership and non-conformity threshold. We evaluate the performance of both of our algorithms in an extensive set of experiments. Code to replicate all of our experiments can be found at https://github.com/ProgBelarus/BatchMultivalidConformal
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge