Privacy-Preserving Race/Ethnicity Estimation for Algorithmic Bias Measurement in the U.S

AI fairness measurements, including tests for equal treatment, often take the form of disaggregated evaluations of AI systems. Such measurements are an important part of Responsible AI operations. These measurements compare system performance across demographic groups or sub-populations and typically require member-level demographic signals such as gender, race, ethnicity, and location. However, sensitive member-level demographic attributes like race and ethnicity can be challenging to obtain and use due to platform choices, legal constraints, and cultural norms. In this paper, we focus on the task of enabling AI fairness measurements on race/ethnicity for \emph{U.S. LinkedIn members} in a privacy-preserving manner. We present the Privacy-Preserving Probabilistic Race/Ethnicity Estimation (PPRE) method for performing this task. PPRE combines the Bayesian Improved Surname Geocoding (BISG) model, a sparse LinkedIn survey sample of self-reported demographics, and privacy-enhancing technologies like secure two-party computation and differential privacy to enable meaningful fairness measurements while preserving member privacy. We provide details of the PPRE method and its privacy guarantees. We then illustrate sample measurement operations. We conclude with a review of open research and engineering challenges for expanding our privacy-preserving fairness measurement capabilities.

Beyond DAGs: Modeling Causal Feedback with Fuzzy Cognitive Maps

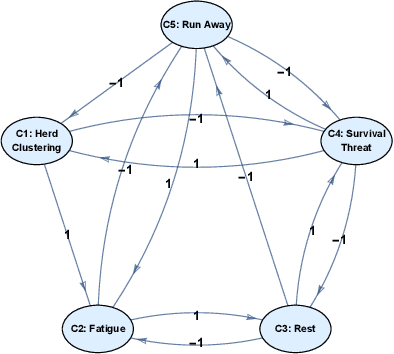
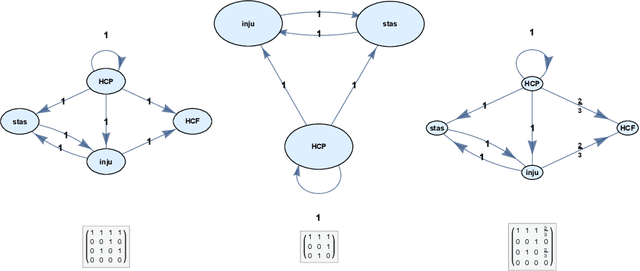
Fuzzy cognitive maps (FCMs) model feedback causal relations in interwoven webs of causality and policy variables. FCMs are fuzzy signed directed graphs that allow degrees of causal influence and event occurrence. Such causal models can simulate a wide range of policy scenarios and decision processes. Their directed loops or cycles directly model causal feedback. Their nonlinear dynamics permit forward-chaining inference from input causes and policy options to output effects. Users can add detailed dynamics and feedback links directly to the causal model or infer them with statistical learning laws. Users can fuse or combine FCMs from multiple experts by weighting and adding the underlying fuzzy edge matrices and do so recursively if needed. The combined FCM tends to better represent domain knowledge as the expert sample size increases if the expert sample approximates a random sample. Many causal models use more restrictive directed acyclic graphs (DAGs) and Bayesian probabilities. DAGs do not model causal feedback because they do not contain closed loops. Combining DAGs also tends to produce cycles and thus tends not to produce a new DAG. Combining DAGs tends to produce a FCM. FCM causal influence is also transitive whereas probabilistic causal influence is not transitive in general. Overall: FCMs trade the numerical precision of probabilistic DAGs for pattern prediction, faster and scalable computation, ease of combination, and richer feedback representation. We show how FCMs can apply to problems of public support for insurgency and terrorism and to US-China conflict relations in Graham Allison's Thucydides-trap framework. The appendix gives the textual justification of the Thucydides-trap FCM. It also extends our earlier theorem [Osoba-Kosko2017] to a more general result that shows the transitive and total causal influence that upstream concept nodes exert on downstream nodes.

Noisy Expectation-Maximization: Applications and Generalizations

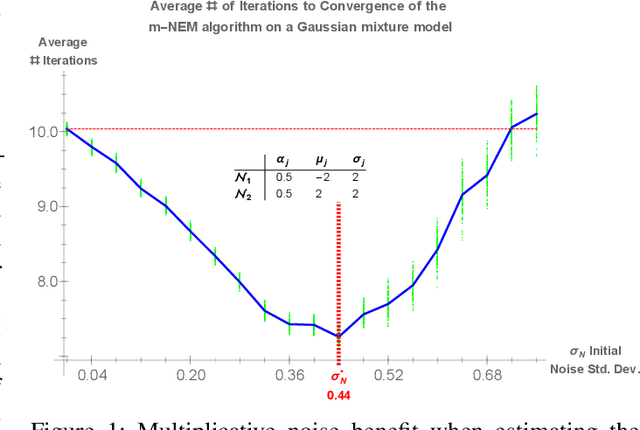
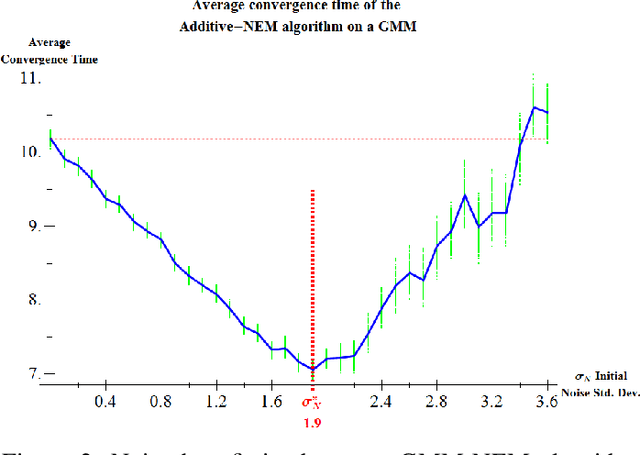
We present a noise-injected version of the Expectation-Maximization (EM) algorithm: the Noisy Expectation Maximization (NEM) algorithm. The NEM algorithm uses noise to speed up the convergence of the EM algorithm. The NEM theorem shows that injected noise speeds up the average convergence of the EM algorithm to a local maximum of the likelihood surface if a positivity condition holds. The generalized form of the noisy expectation-maximization (NEM) algorithm allow for arbitrary modes of noise injection including adding and multiplying noise to the data. We demonstrate these noise benefits on EM algorithms for the Gaussian mixture model (GMM) with both additive and multiplicative NEM noise injection. A separate theorem (not presented here) shows that the noise benefit for independent identically distributed additive noise decreases with sample size in mixture models. This theorem implies that the noise benefit is most pronounced if the data is sparse. Injecting blind noise only slowed convergence.