Noisy Expectation-Maximization: Applications and Generalizations
Paper and Code
Jan 12, 2018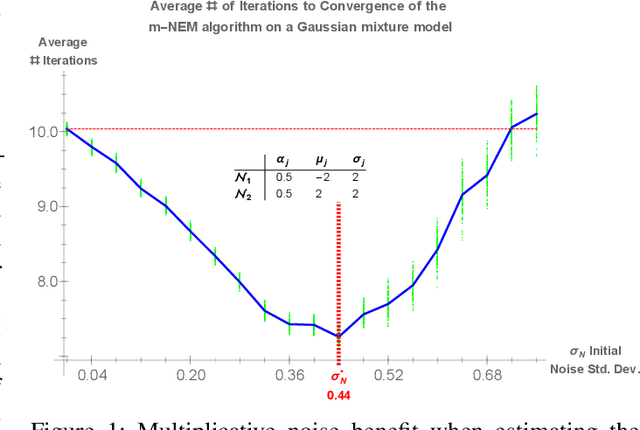
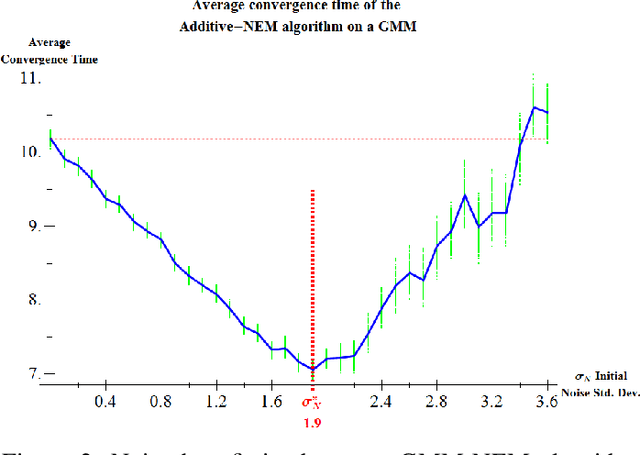
We present a noise-injected version of the Expectation-Maximization (EM) algorithm: the Noisy Expectation Maximization (NEM) algorithm. The NEM algorithm uses noise to speed up the convergence of the EM algorithm. The NEM theorem shows that injected noise speeds up the average convergence of the EM algorithm to a local maximum of the likelihood surface if a positivity condition holds. The generalized form of the noisy expectation-maximization (NEM) algorithm allow for arbitrary modes of noise injection including adding and multiplying noise to the data. We demonstrate these noise benefits on EM algorithms for the Gaussian mixture model (GMM) with both additive and multiplicative NEM noise injection. A separate theorem (not presented here) shows that the noise benefit for independent identically distributed additive noise decreases with sample size in mixture models. This theorem implies that the noise benefit is most pronounced if the data is sparse. Injecting blind noise only slowed convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge